大家好,我是闪光蜗牛,今天来分享一个真实案例。
前两天跟朋友聊到了圆弧输出,朋友那边的一种机床在走大于180°的圆弧时,如果此时以-R输出,则会发生过切可能。而如果以象限点的方式输出圆弧,则正常切削。

蜗牛也初次听说这样的情况,思考了一下,可以直接用象限的方式输出所有的圆弧,便可解决过切问题。 不过这样一来,整圆就无法输出IJK了吗?作为UG爱好者的一员,显然不能对这样的情况无动于衷。
蜗牛通过分析,觉得可以从两个方向入手实现目的。
方向一:添加预读指令,判断mom_nxt_arc_angle的值是否符合输出条件,然后对变量mom_kin_arc_output_mode进行定义,其值可为FULL_CIRCLE或QUADRANT。
方向二:通过已知条件计算圆弧以象限方式运动的过程。 本贴旨在对上述方向二进行思路及做法详解。
首先呢,在圆弧运动事件里添加一些块,适配R的输出环境。
Tips:不要忘记把IJK定义为非模态哦,R也要定义为强制输出。
接下来,我们在输出IJK的块上右键,添加一个条件,输入以下的代码。
#ijk
global mom_arc_angle
global mom_arc_radius
if {[EQ_is_equal_tol $mom_arc_angle 360 0.0001]} {
return 1
} else {
return 0
}
注意这里为什么要用到“EQ_is_equal_tol”这个过程呢,相信有读者会不太明白。这个过程可以帮助我们更便捷的管理误差,也是一个直观、安全的后处理的优质体现。0.0001便是此时允许的最大误差。蜗牛在这里精确了四位小数,这个可以根据实际情况自行调整。如果读者有兴趣可以引入弦高作为参数,同样能有效的对误差进行控制。
然后同样的,对输出R的块也要添加一个条件,输入以下代码。
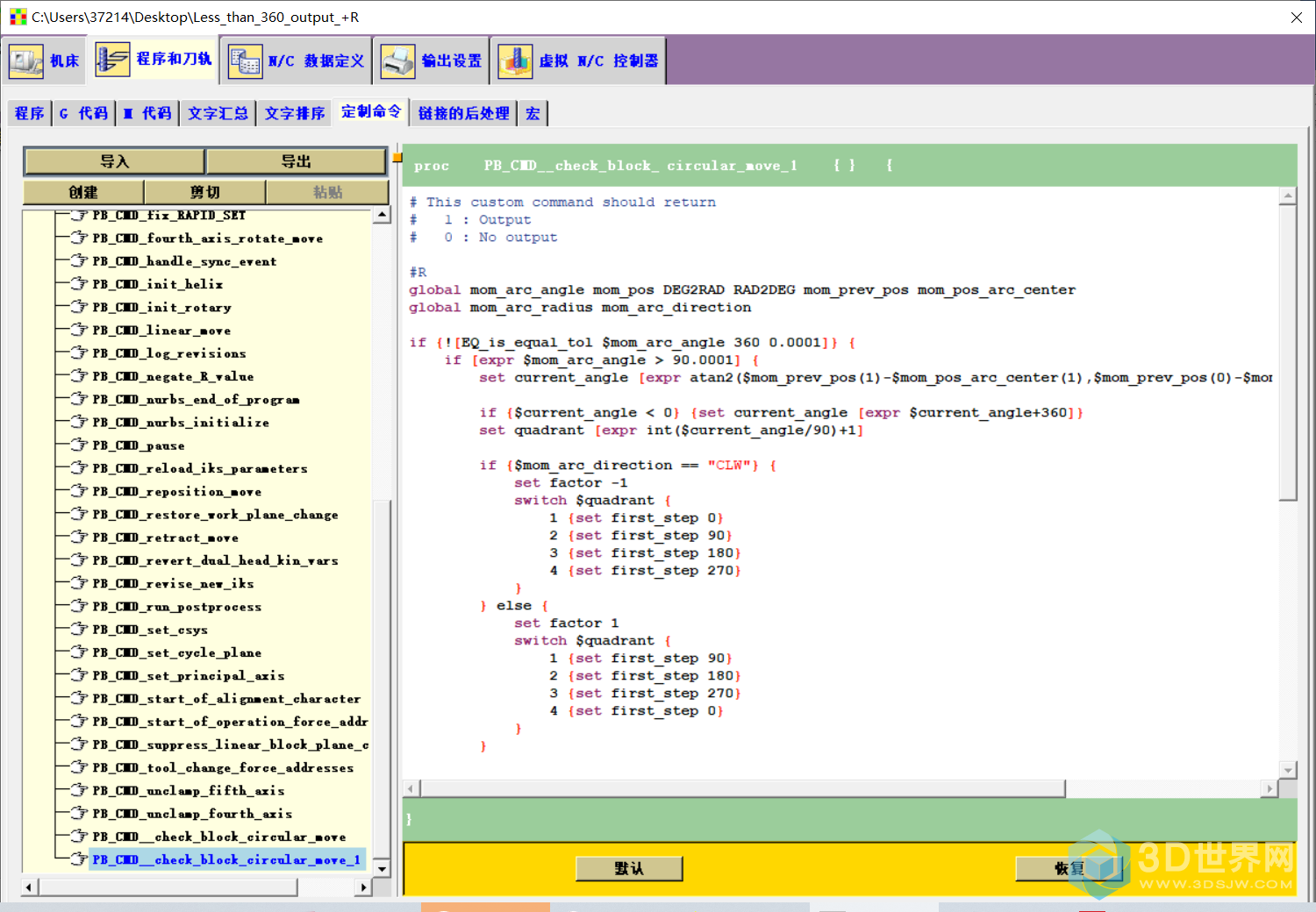
#R
global mom_arc_angle mom_pos DEG2RAD RAD2DEG mom_prev_pos mom_pos_arc_center
global mom_arc_radius mom_arc_direction
if {![EQ_is_equal_tol $mom_arc_angle 360 0.0001]} {
if [expr $mom_arc_angle > 90.0001] {
set current_angle [expr atan2($mom_prev_pos(1)-$mom_pos_arc_center(1),$mom_prev_pos(0)-$mom_pos_arc_center(0))*$RAD2DEG]
if {$current_angle < 0} {set current_angle [expr $current_angle+360]}
set quadrant [expr int($current_angle/90)+1]
if {$mom_arc_direction == "CLW"} {
set factor -1
switch $quadrant {
1 {set first_step 0}
2 {set first_step 90}
3 {set first_step 180}
4 {set first_step 270}
}
} else {
set factor 1
switch $quadrant {
1 {set first_step 90}
2 {set first_step 180}
3 {set first_step 270}
4 {set first_step 0}
}
}
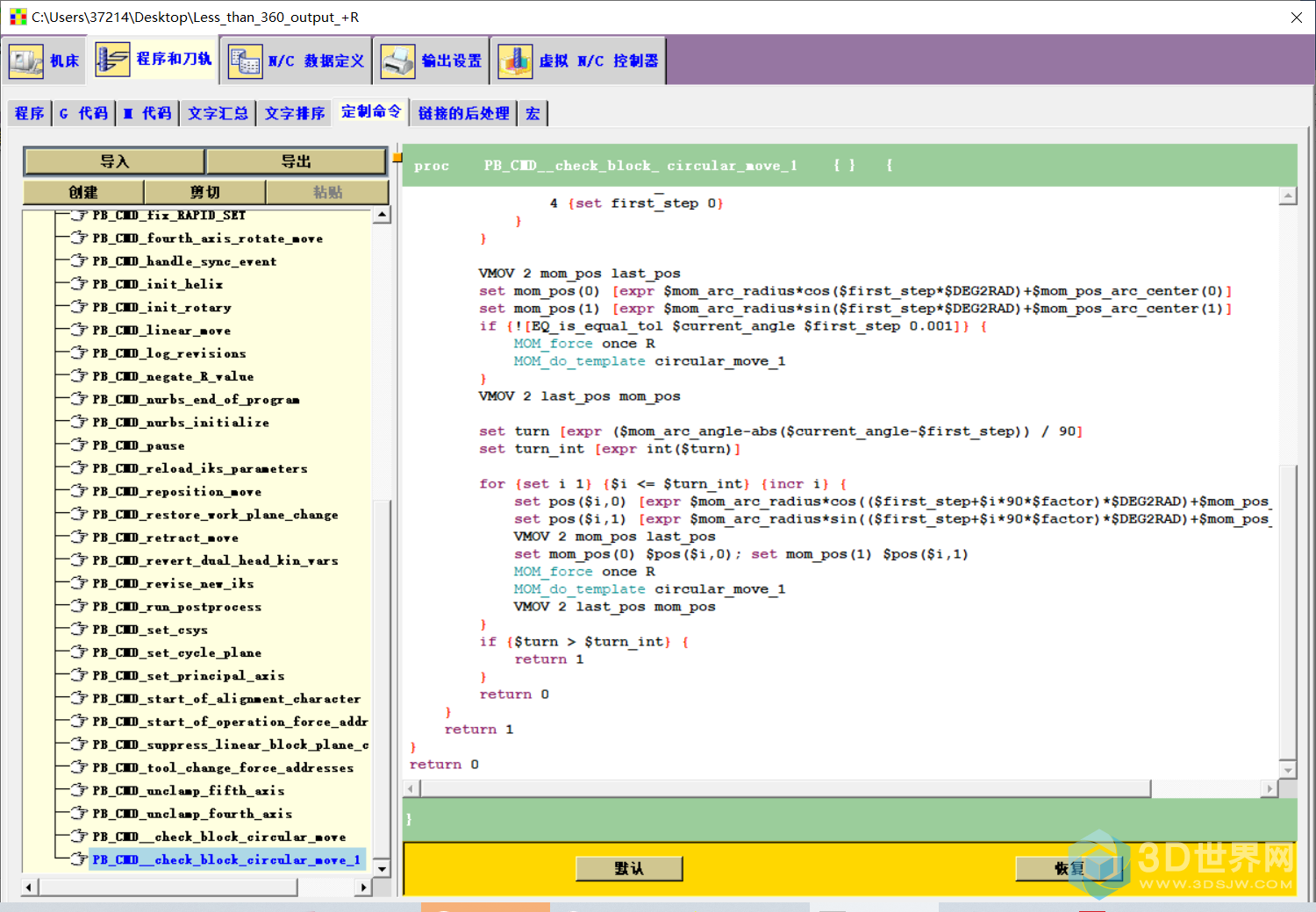
VMOV 2 mom_pos last_pos
set mom_pos(0) [expr $mom_arc_radius*cos($first_step*$DEG2RAD)+$mom_pos_arc_center(0)]
set mom_pos(1) [expr $mom_arc_radius*sin($first_step*$DEG2RAD)+$mom_pos_arc_center(1)]
if {![EQ_is_equal_tol $current_angle $first_step 0.001]} {
MOM_force once R
MOM_do_template circular_move_1
}
VMOV 2 last_pos mom_pos
set turn [expr ($mom_arc_angle-abs($current_angle-$first_step)) / 90]
set turn_int [expr int($turn)]
for {set i 1} {$i <= $turn_int} {incr i} {
set pos($i,0) [expr $mom_arc_radius*cos(($first_step+$i*90*$factor)*$DEG2RAD)+$mom_pos_arc_center(0)]
set pos($i,1) [expr $mom_arc_radius*sin(($first_step+$i*90*$factor)*$DEG2RAD)+$mom_pos_arc_center(1)]
VMOV 2 mom_pos last_pos
set mom_pos(0) $pos($i,0); set mom_pos(1) $pos($i,1)
MOM_force once R
MOM_do_template circular_move_1
VMOV 2 last_pos mom_pos
}
if {$turn > $turn_int} {
return 1
}
return 0
}
return 1
}
return 0
相信读者在这里已经明白所有的思路了:
通过圆心角mom_arc_angle判断输出环境——计算圆弧运动前于笛卡尔坐标系下的位置——判断下一个象限点并输出圆弧——得出过程点位并输出——输出最后的点位,完成圆弧运动。
这样看来是不是很简单呢。
NX后处理给我们提供了广阔的空间,可以任我们的思想翱翔。
最后附上后处理及测试图档。 温馨提示,附件的后处理只是为了展示功能从后处理库中新建的,不能直接上机哦。
|