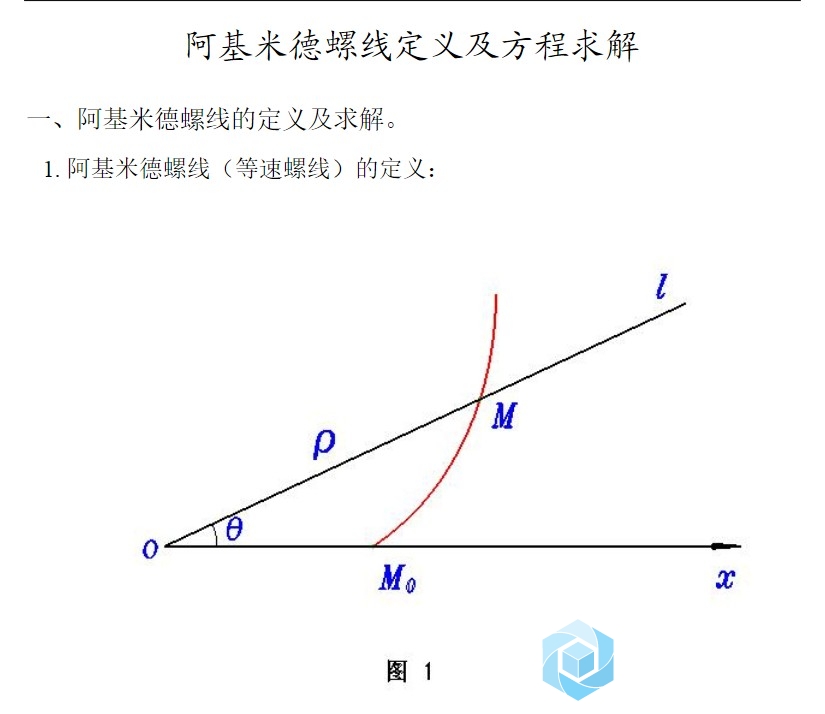
这个思路来源一个数学公式,阿基米德螺旋线。
编程效果如下图:
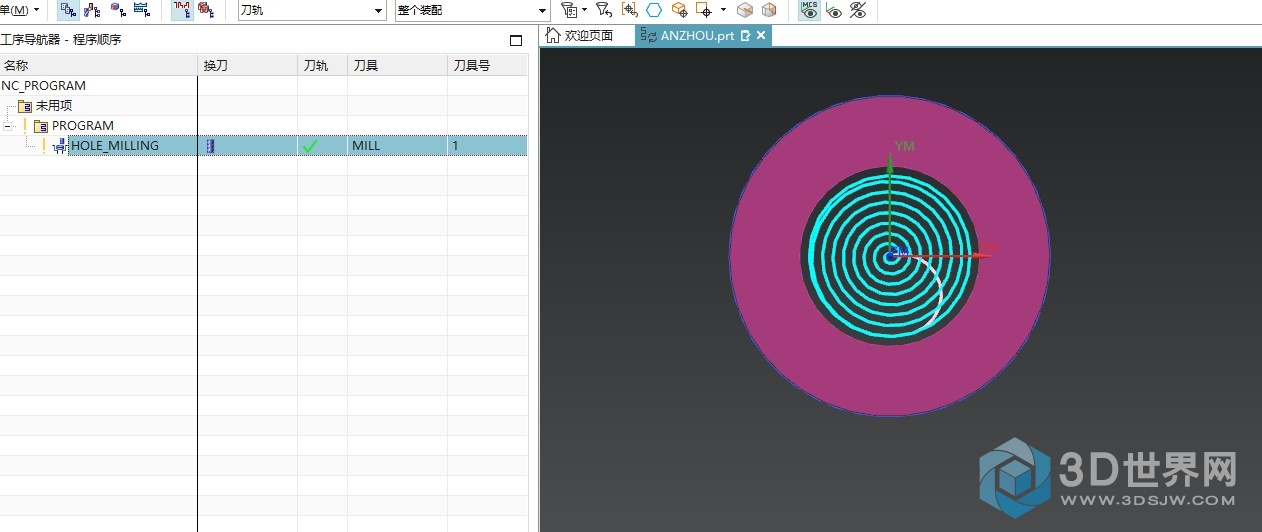
切削模式平面螺旋:
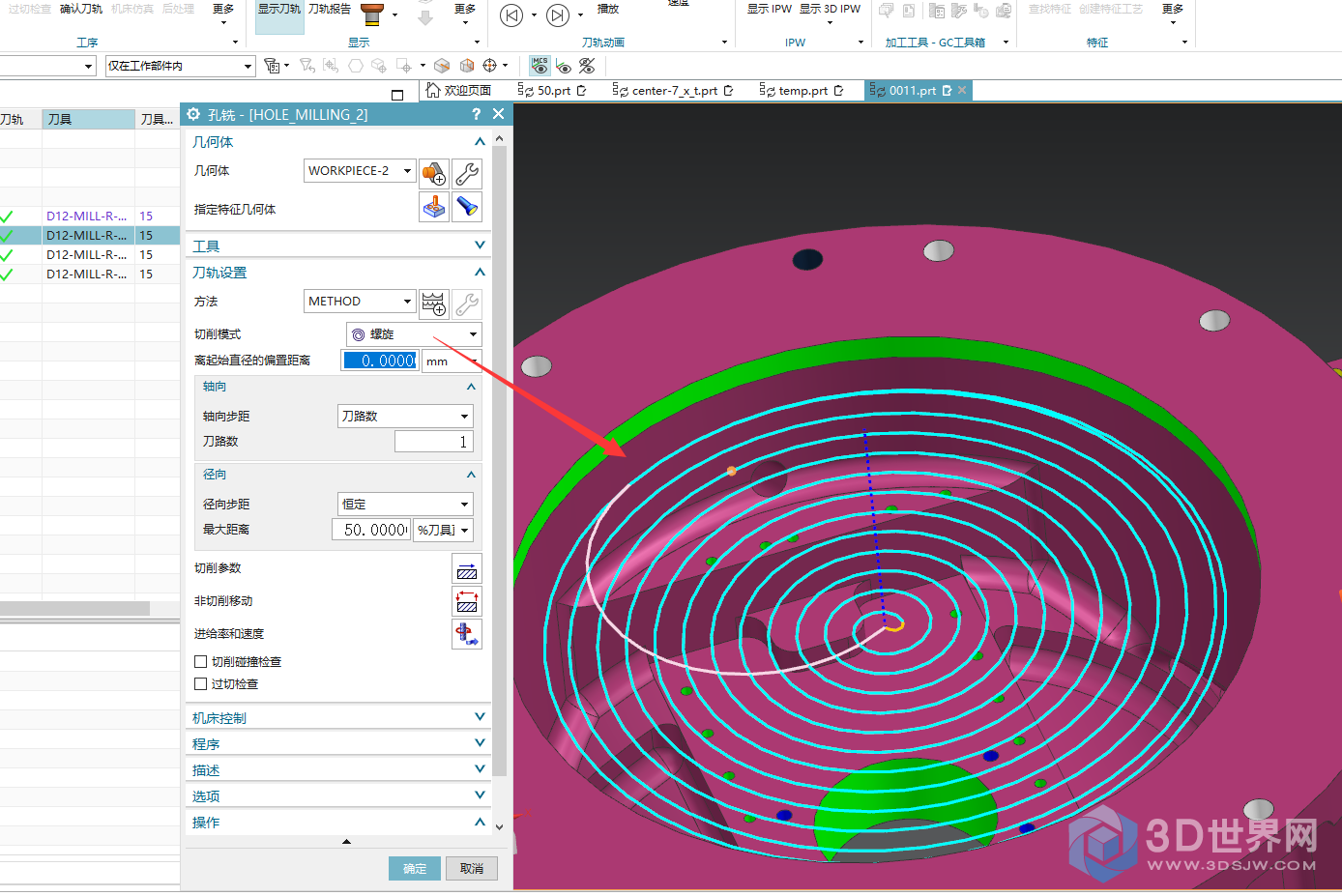
后处理程序效果:G2输出。
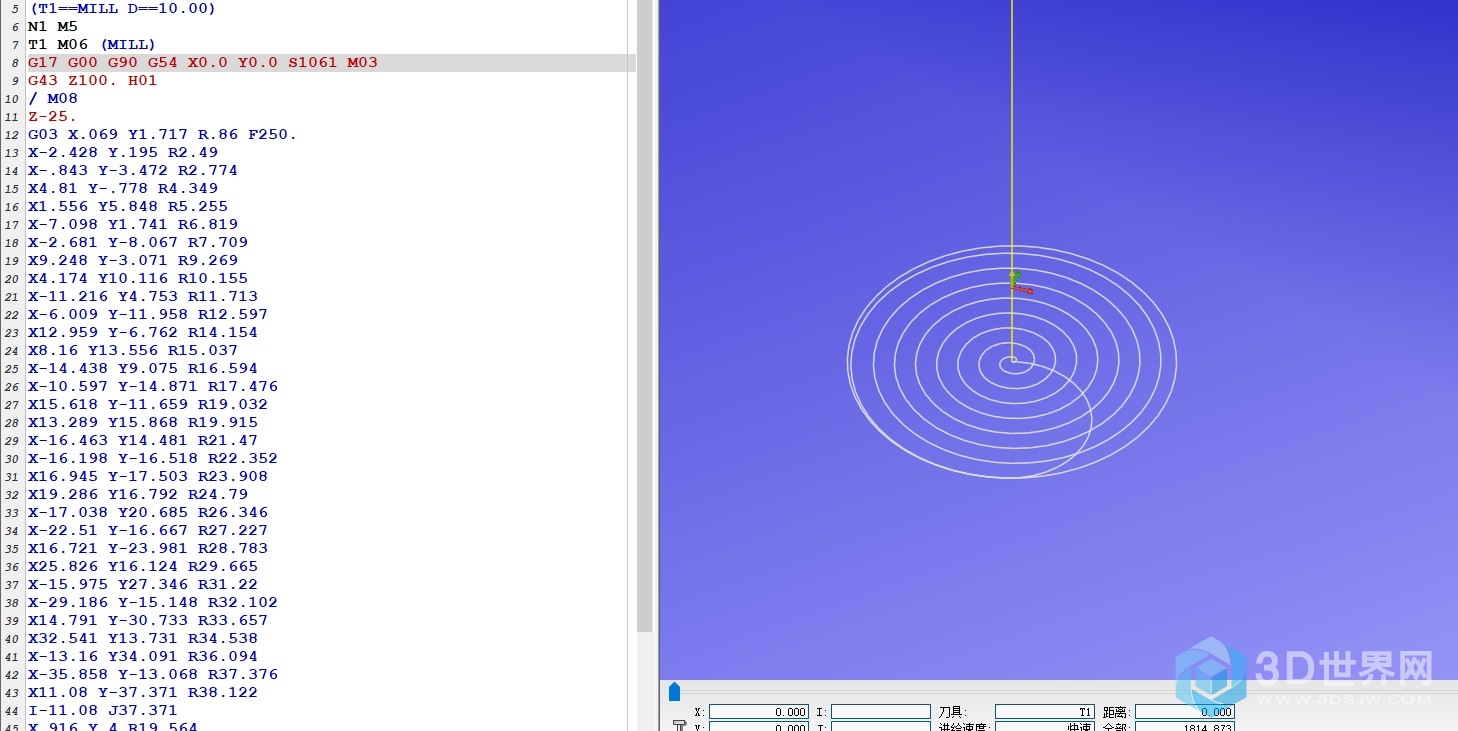
在此以完全了解程序的效果,这个程序对于一个NX后处理爱好者来说,不能墨守成规,前进是永无止境的,那么解决这样规律曲线参考阿基米德螺旋线方程,很好的完成了简化程序目的,使程序整体结构性更强,既高大上又不失简约,也符合设计者的初衷以及科学的理念。
1:方程原理如下
它的极坐标方程为:r = aθ  
   这种螺线的每条臂的距离永远相等于 2πa   笛卡尔坐标方程式为:   r=10*(1+t)   x=r*cos(t*360)   y=r*sin(t*360)



2:编写机床宏程序
发那科宏如下:

海德汉宏如下:

以上宏程序我已经优化,开始用R判断是否到达终点,后面觉得R的精度不好,最后用角度去做判断,为什么这么做呢,因为R半径是10进制 而角度是60进制,所以角度的精度更好! 也取决于步进角的大小,这其中需要处理一个整除情况,那么步进角用科学计数法来执行步进角,使之 绝对整除!也可以双向判断,用R的同时也用角度,这样会解决一个问题就是,当你设置了重叠不会过切,因为直径随着角度的变化而增大,所以这样从而保证刀路轨迹的正确性! 3:NX后置的设置注意事项
判断策略的变量 mom_region_cut_method
开始直径 X²+Y²=Z²
起始角度 atan2(y,x)
终止直径 X²+Y²=Z²
终止角度 angle(s)+angle(i)
螺旋方向 mom_arc_direction
总结:
做一个判断和其他策略不会冲突即可!作者已经加入实际应用中,取得了不错的效果,分享思路以及过程,
目的就是程序最优化,简约但不简单!优化发那科的内存不足的问题! 其实很多规律的刀路都是可以作为宏。 后处理在于折腾,技术也是如此! 作为一名爱好者,独乐不如众乐! 安周 2020-05-30
|