Creo3.0 理论基础

大师兄*

有限元方法
       有限元方法 (FEM) 是一种将具有未知结构行为的复杂几何细分为具有已知结构行为的有限数量的简单几何元素的方法。在元素边界，位移等于相邻元素，进而得出矩阵方程。该方程通过数值求解，然后通过后处理器以图形方式显示结果。
传统方法使用偏微分方程表达问题。这种偏微分方程通常是简化假设条件 (如线性弹性材料或较小的位移) 后得出的结果。这种方程可能无法求出解，因为几何与载荷过于复杂。因此需要数值解，而提供这种解的方法就是 FEM。
FEM 包括以下内容：
标识几何与载荷工况。

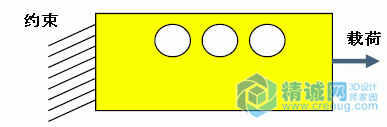
       将几何网格化为有限数量的元素 - 网格是节点与元素的排列。有限元可以是四边形和/或三角形。节点是元素互相连接的位置。通常，网格越精细，结果便越精确。

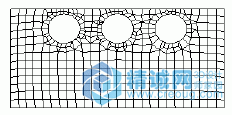
        计算每个元素的结构行为 - 在应力分析问题中，所用因变量是与参考位置 (通常是卸载位置) 之间的位移。在热分析问题中，所用因变量是温度。

       使每个元素的行为与其相邻元素相关 - 在有限元中，在元素节点计算位移。通过合并网格中的所有元素，可以得出一个联立线性代数方程组。
       求出所产生的位移矩阵方程组的数值解 - 计算出位移后，通过对位置求导还可计算出应变 (每单位长度位移)。如果需要应力，可根据应变进行计算。
       如果位移场的空间变化插值多项式在元素内成线性，则内部应变与应力均恒定。此外，应力在元素内部仅为连续 (平滑)。在与相邻元素形成的边界处，应力可能会变得不连续 (跳跃)。通常，在后处理器中通过不同求平均方法对此差值进行平滑处理。在求解过程中，此差值还可用于误差估计和收敛改善。Simulate 将超级收敛应力用于此目的 (在后续模块中进行描述)。

h 版和 p 版有限元
       通过细化同类元素的网格或提高每个元素中的位移场精度，可改善有限元分析的结果。最初可使用一定数量的分析三角来划分 (或网格化) 简单矩形。

       目前使用两种有限元方法来演示数值解收敛。h 版和 p 版有限元方法是将自由度 (dof) 添加到模型的两种不同方法。
       h 方法 - h 方法使用同类元素的细化网格改善结果。此方法是指降低元素的特征长度 (h)，以在不更改所用元素类型的情况下，将每个现有元素分成两个或多个元素。

        p 方法 - p 方法通过使用相同网格，但却提高各元素中的位移场精度，来改善结果。此方法是指在不更改所用元素的数量的情况下，增大最高阶完整多项式 (p) 的阶次。

       p 版使用高阶多项式 (Simulate 中所用的最大阶数为 9)，这与传统有限元 (h 方法) 中所用的线性函数 (有时为四次或三次函数) 相反。可能仅需分析一次网格化几何，即可确定解是否已收敛。对于 h 方法，必须创建一系列连续细化网格，才能得出趋于正确结果的收敛。在位移梯度无法由低阶多项式近似表示的情况下，元素阶数越高，结果便越精确。通常，在数值噪声再次降低解的质量之前，网格越精细，结果质量便会越高。

123456*

我要系统学习一下

心已停(#‵′)靠

与人分享是一种奉献和享受！