|
|
本帖最后由 gsmfxsmy 于 2019-1-22 12:48 编辑
其实拧魔方用装配序列相对简单,但如果拧个几万步,运动仿真容易些。效果如下,因为嫌烦,缺了8个角,但原理无差,(倒放是复原,正放是打乱)
基本原理如下:
用6个轴来转动,不能同时转
魔方26个块通过球面副与圆心约束
26个块之间用3D碰撞
(为了降低碰撞的数量,只添加了与6个“轴链接的方块”和12个“十字线上的方块”之间的72个碰撞)
将碰撞的数量从650个降为72个
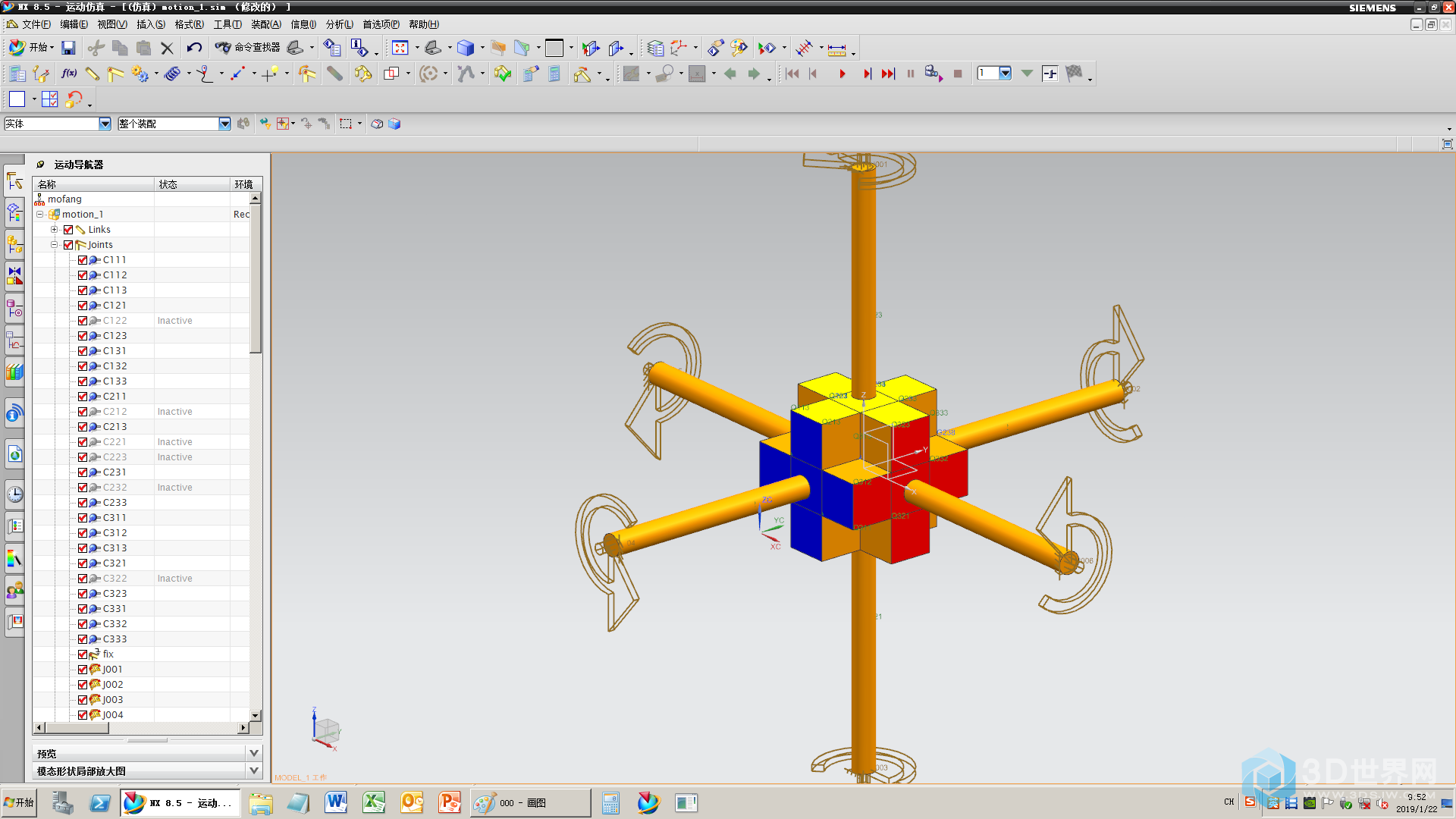
整体过程如下
1、新建一个方块(10*10*10)
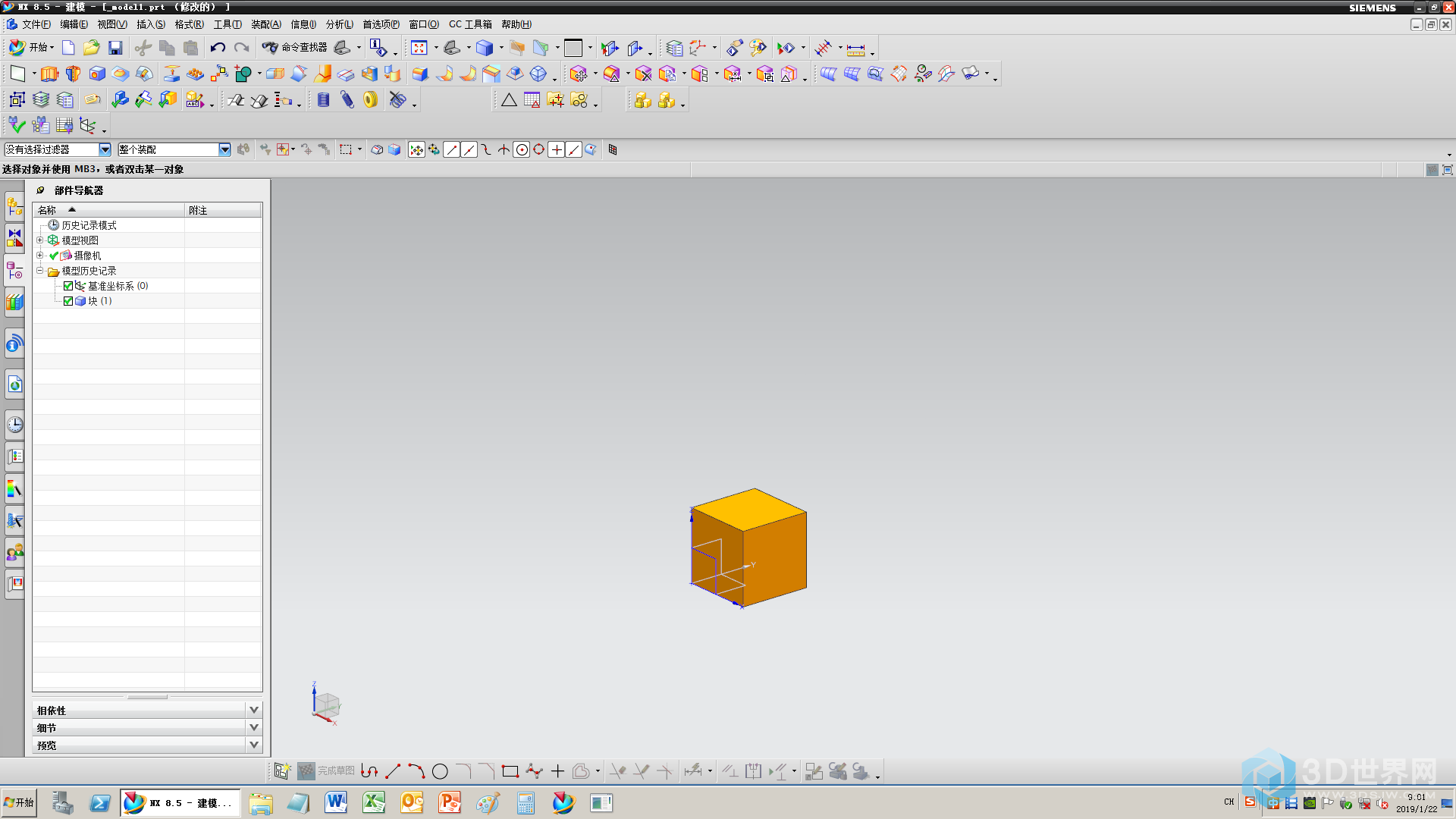
2、阵列3*3
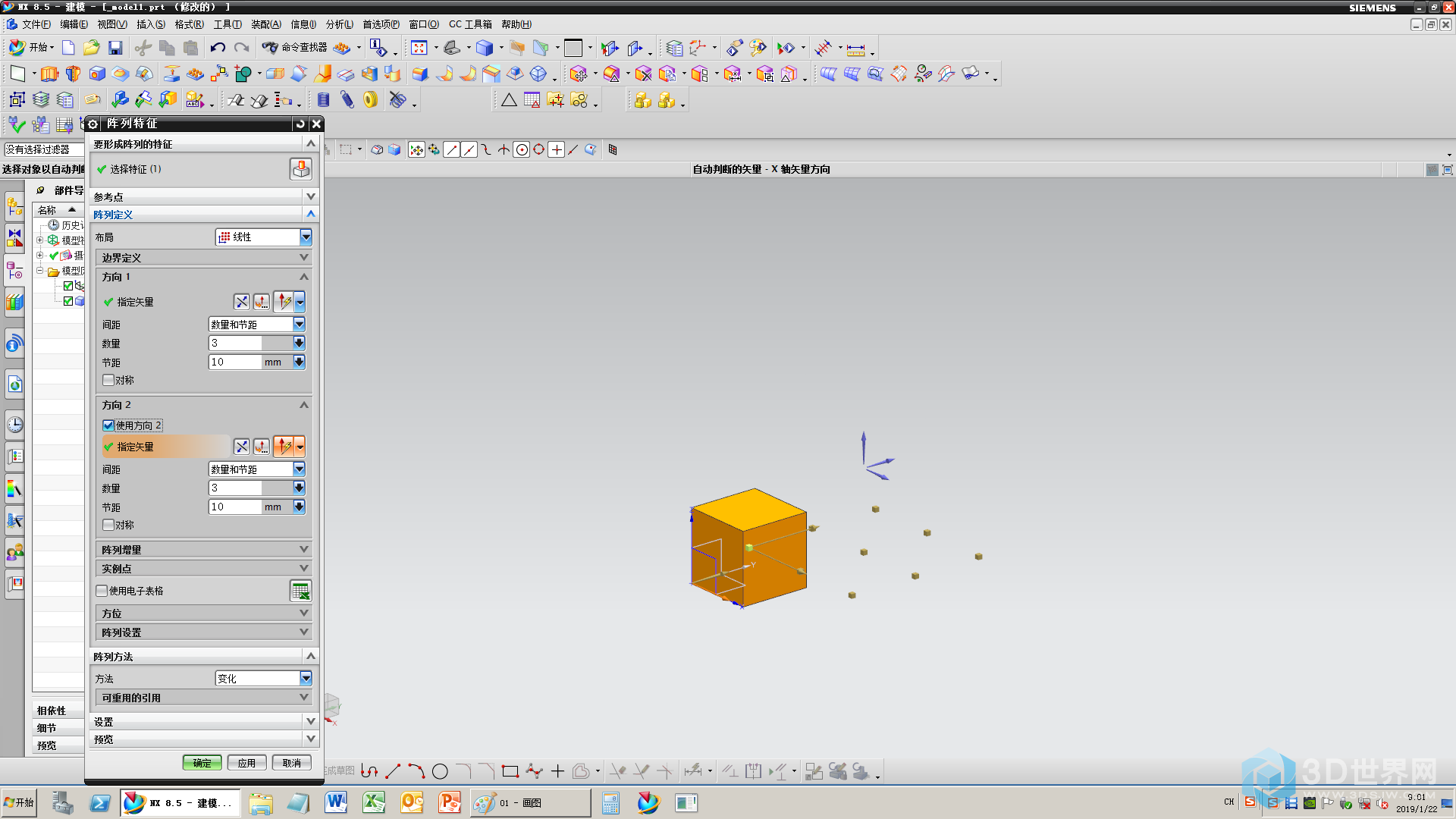
3、阵列3排
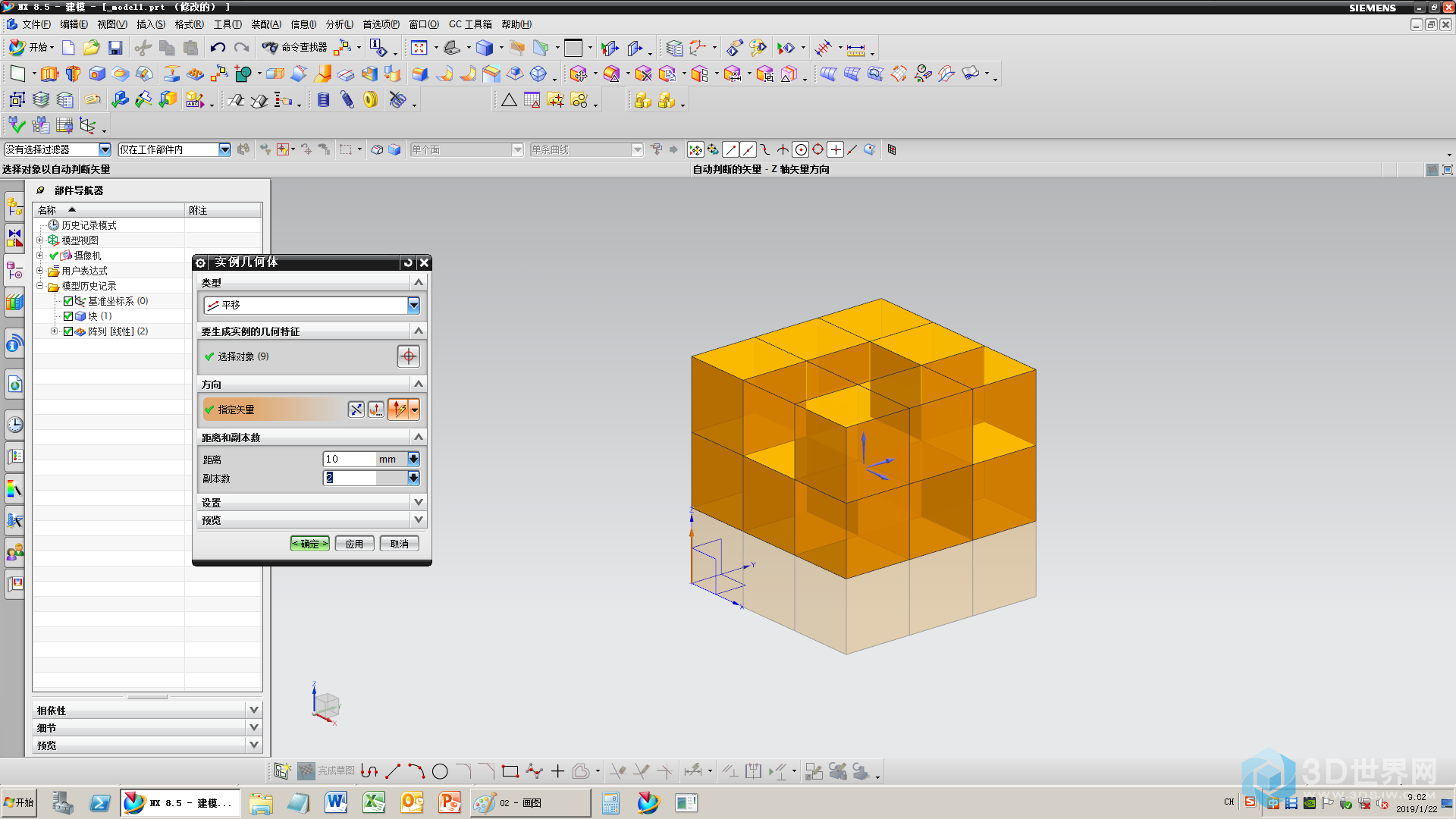
4、将坐标轴从(0,0,0,)点移至(15,15,15,)
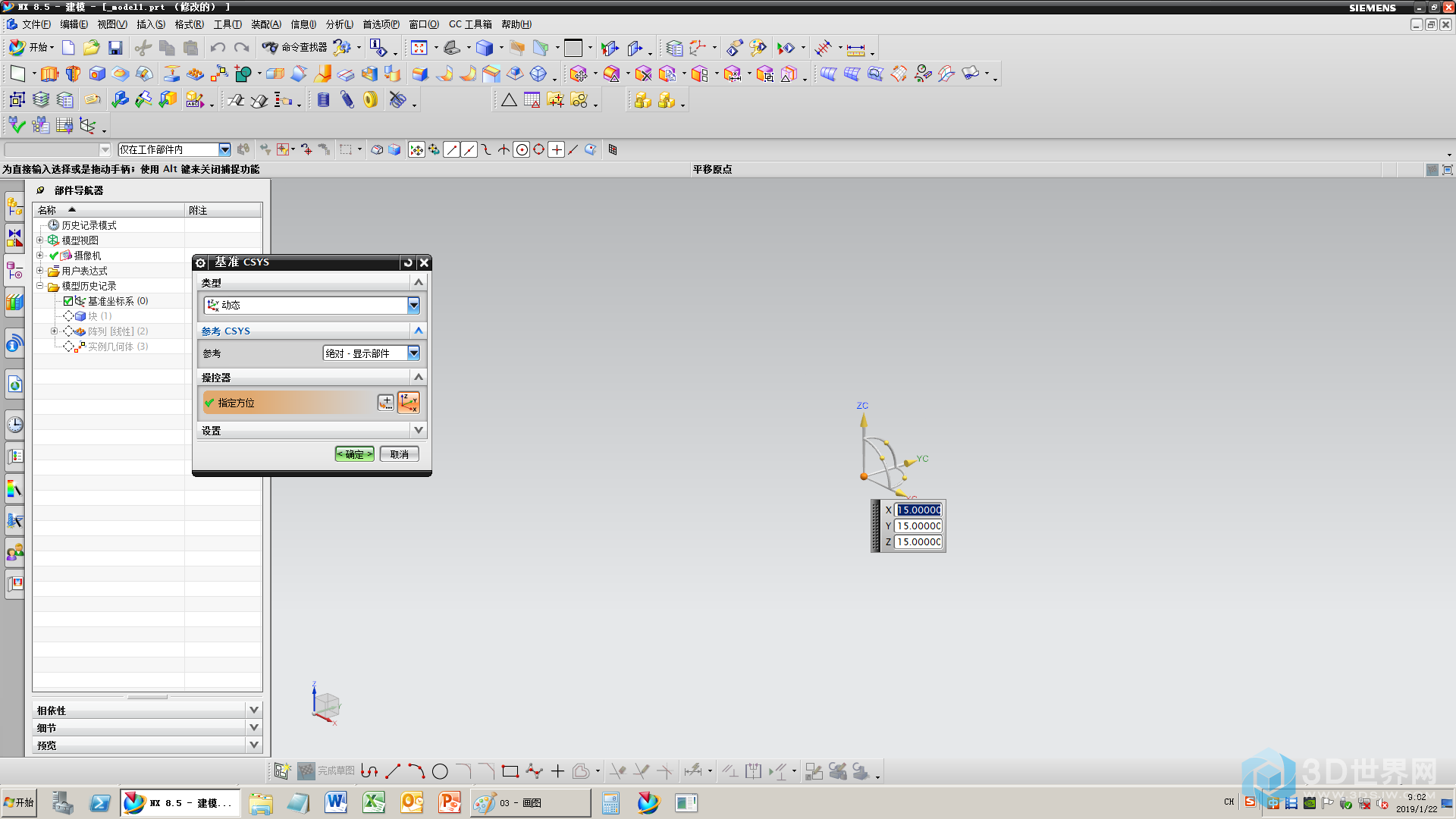
5、移动坐标轴之后的样子
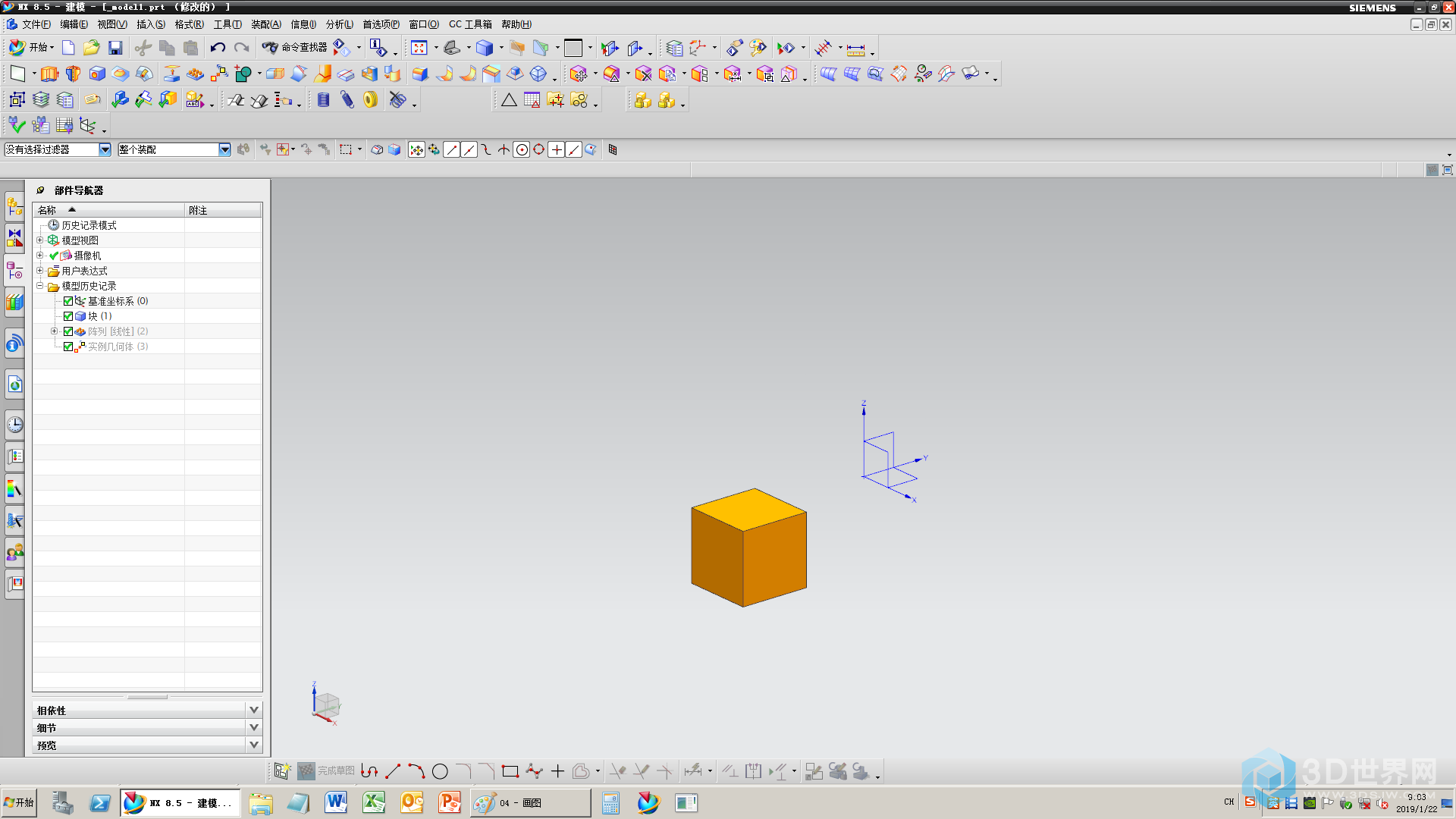
6、在坐标轴原点加个球
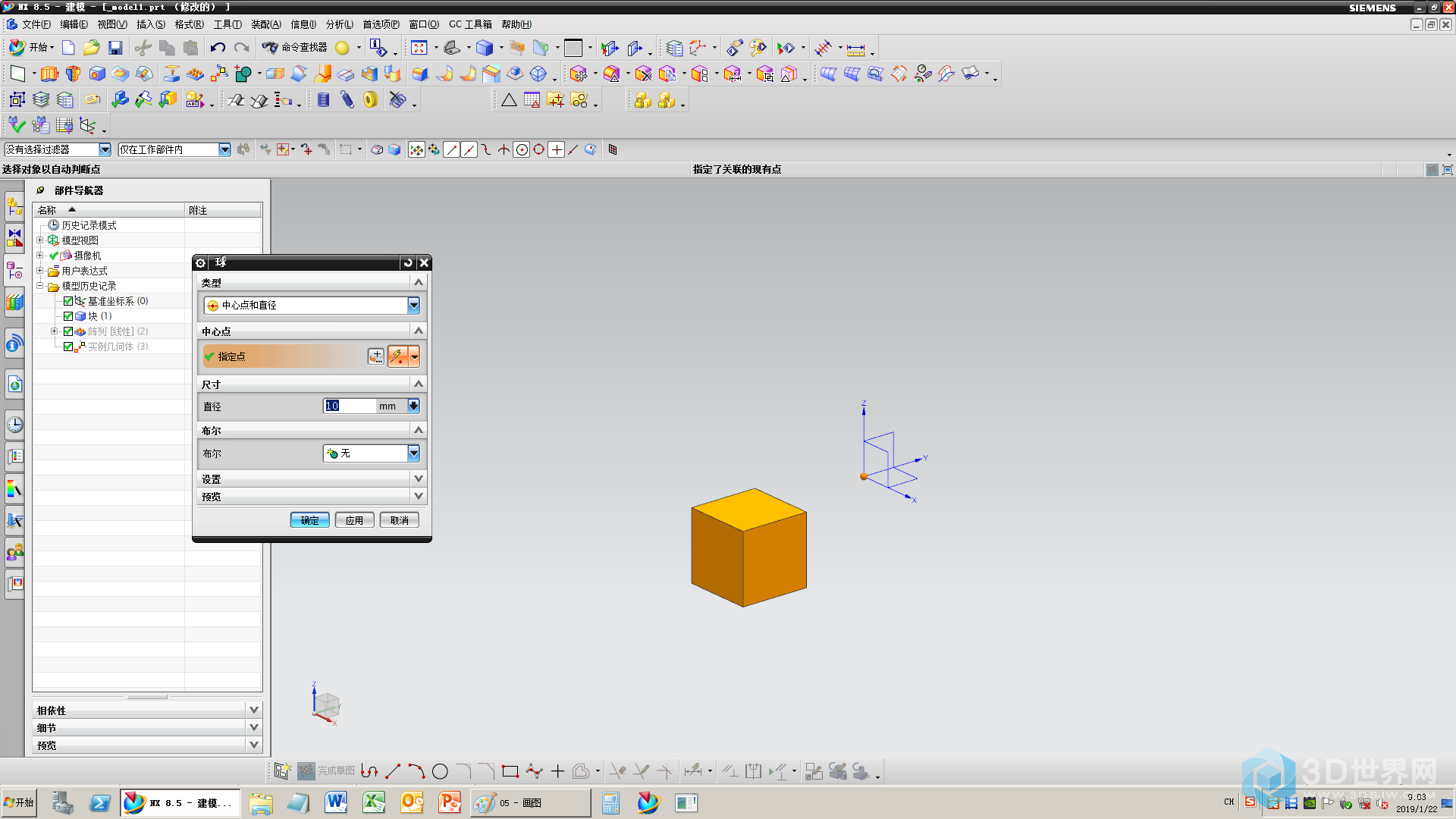
7、将球切一半(神助攻的一步,减少添加圆球副的工作量)
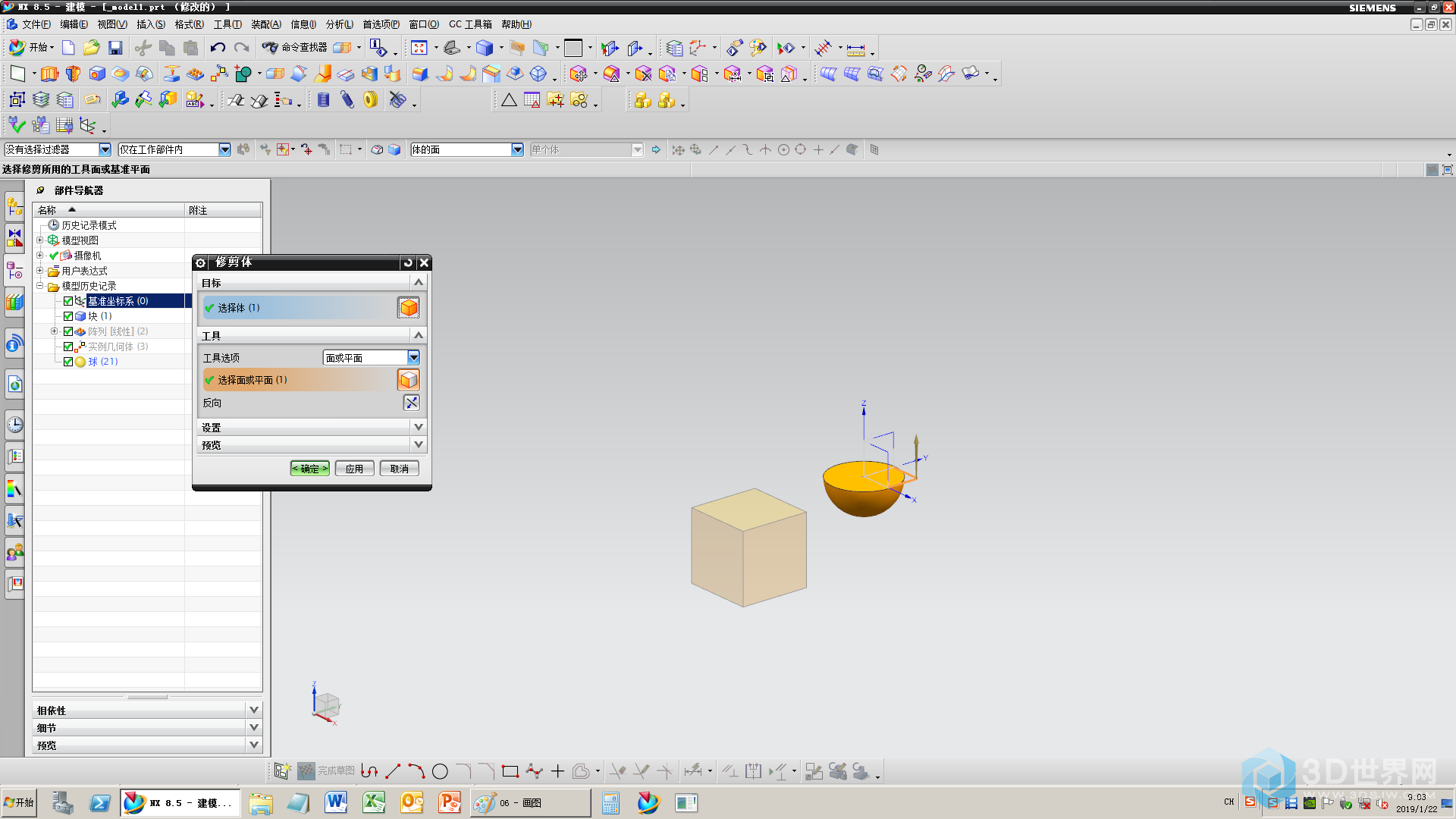
8、添加轴
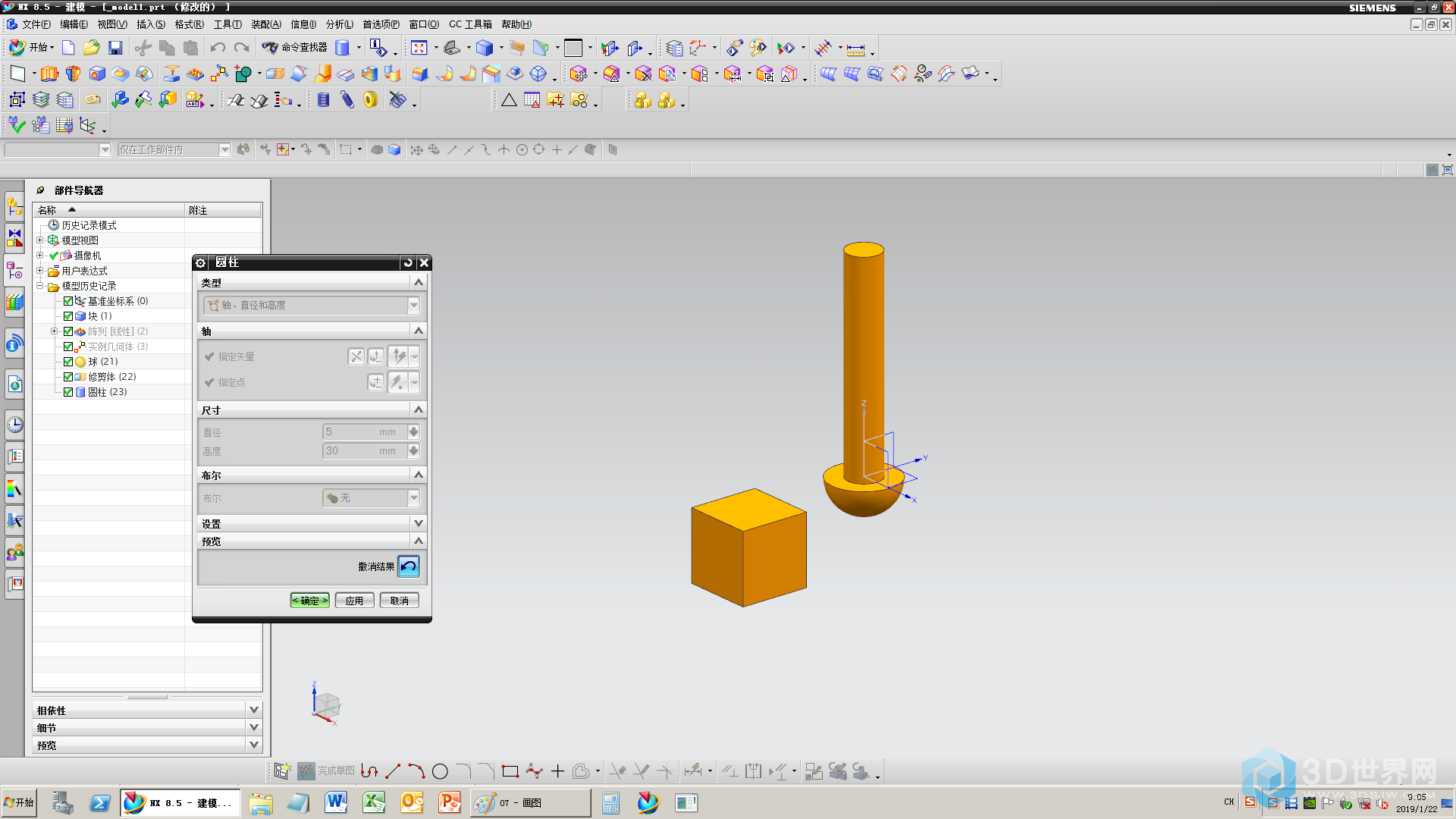
9、1个轴变4个轴
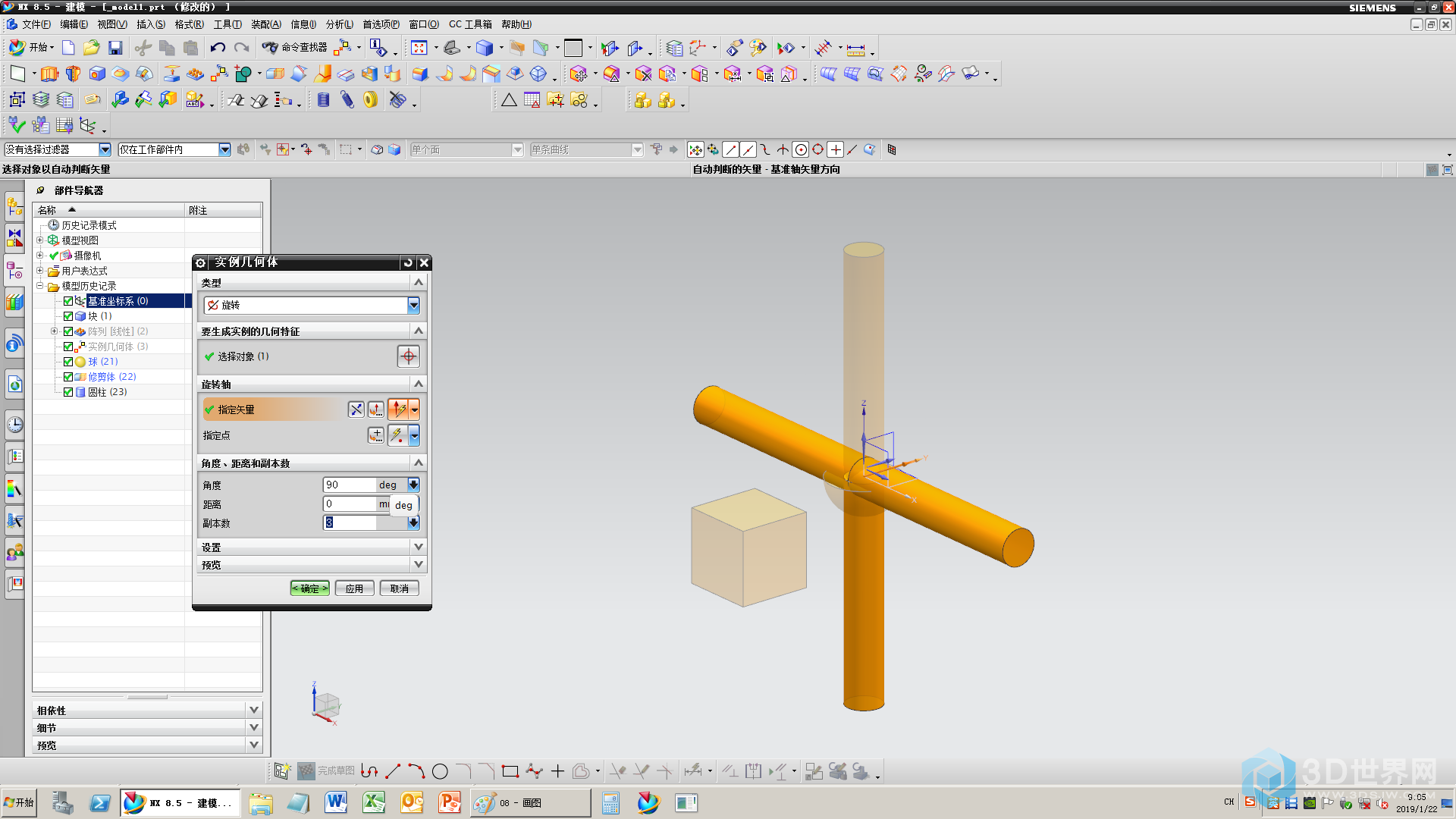
10、4个轴变6个轴
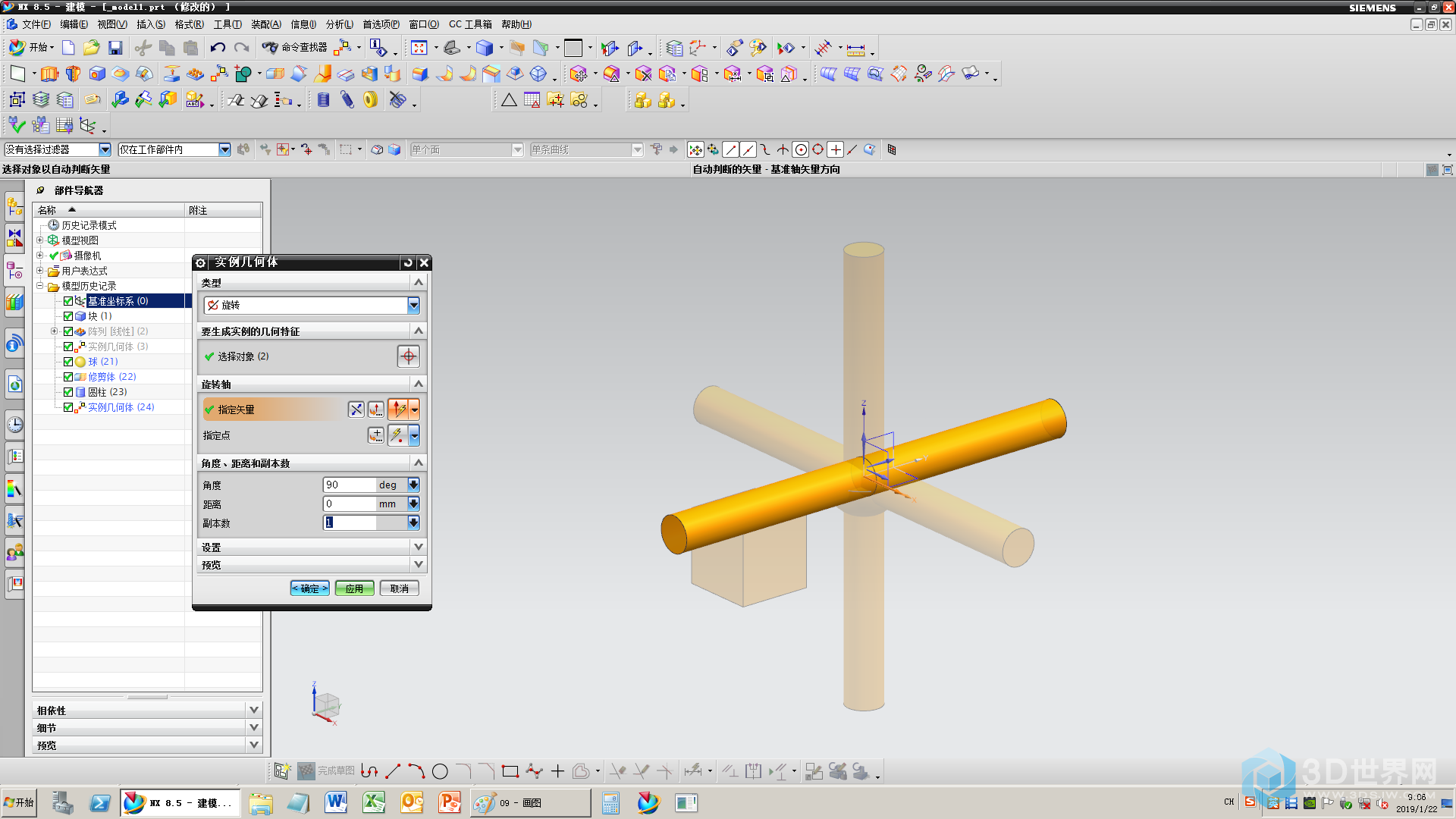
11、完成魔方的模型
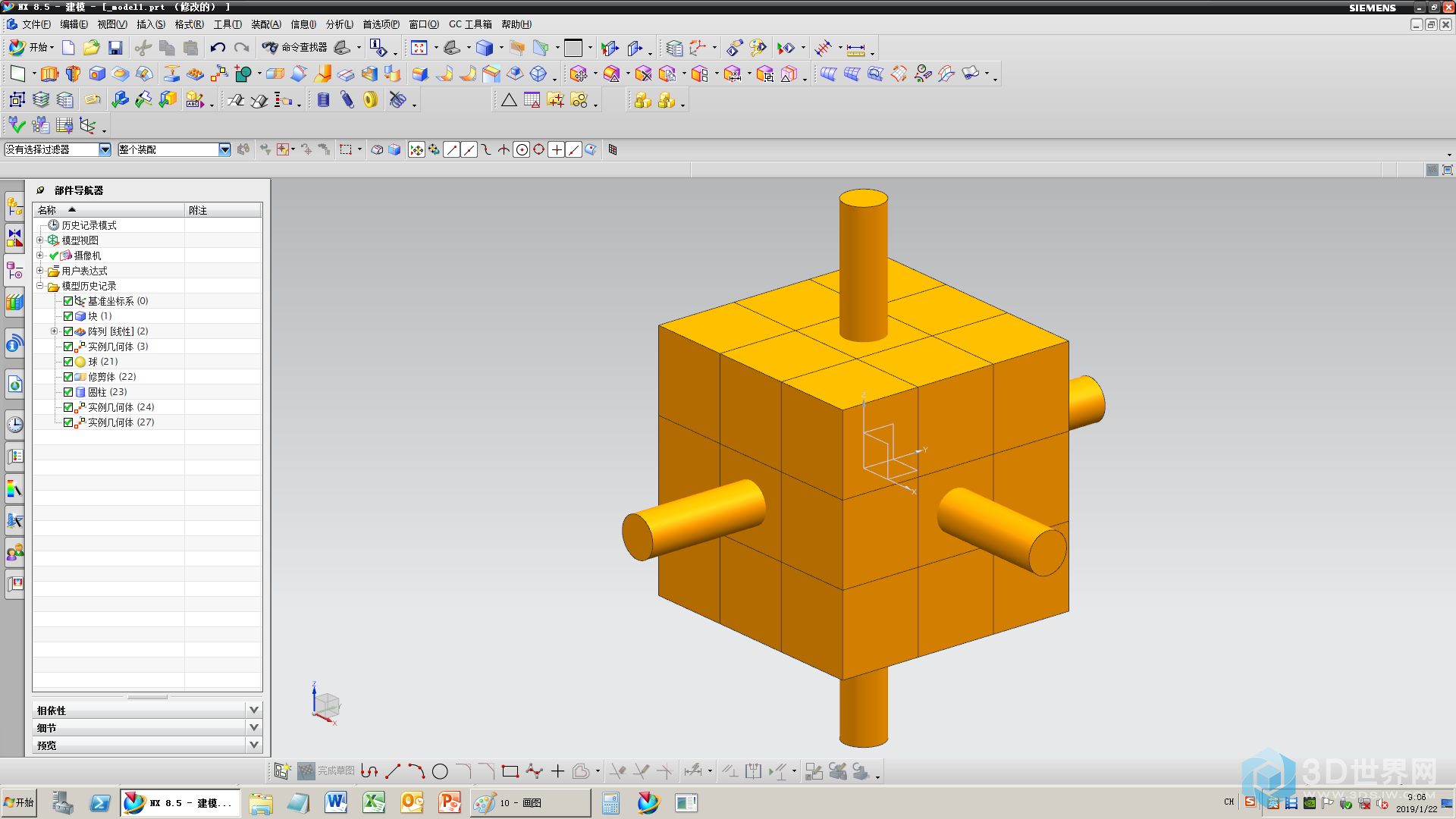
12、按下图给魔方上色
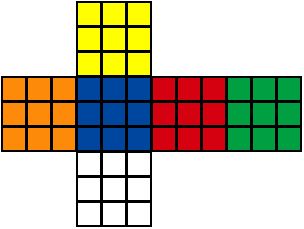
13、选面上色
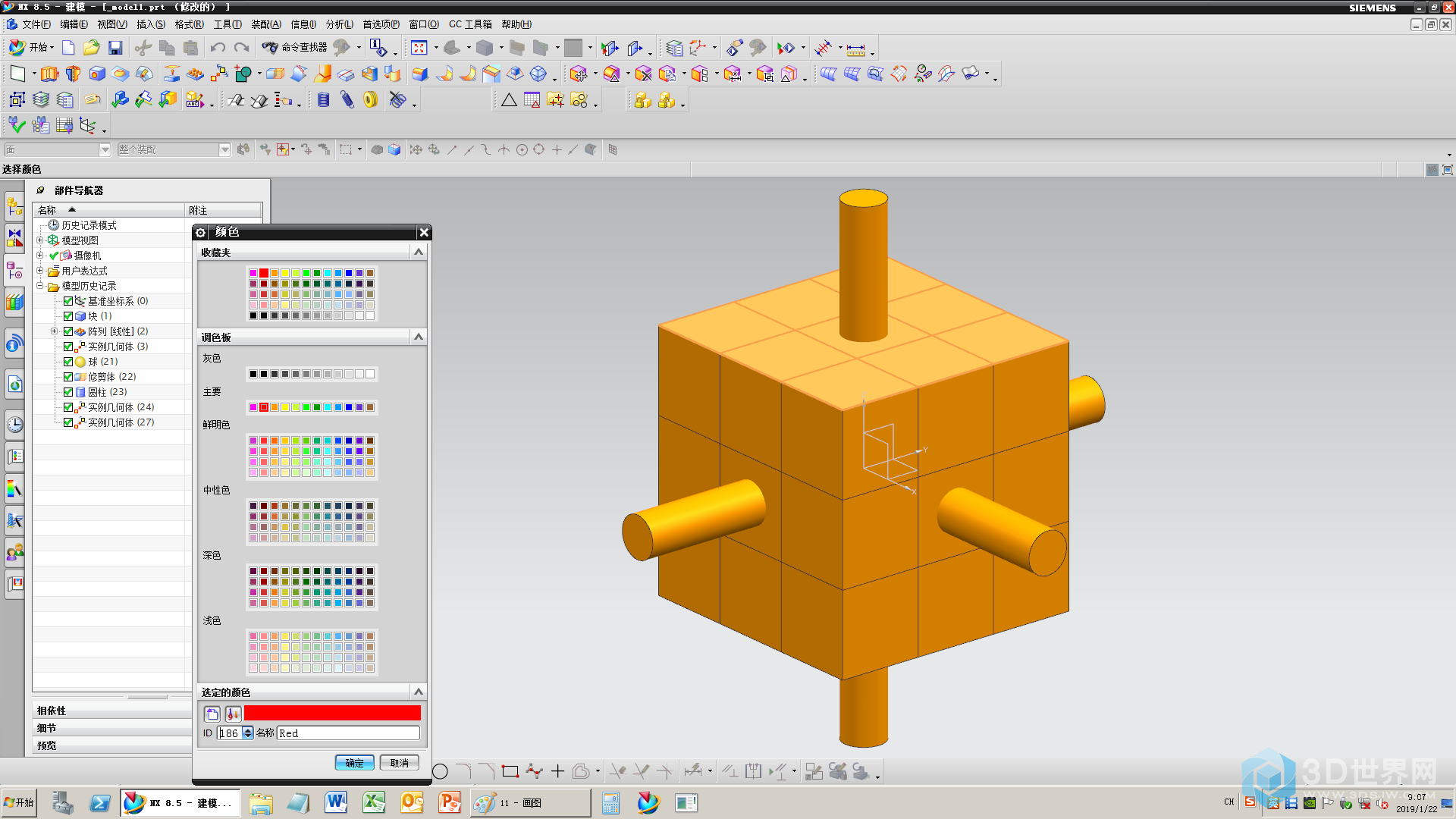
14、完成上色
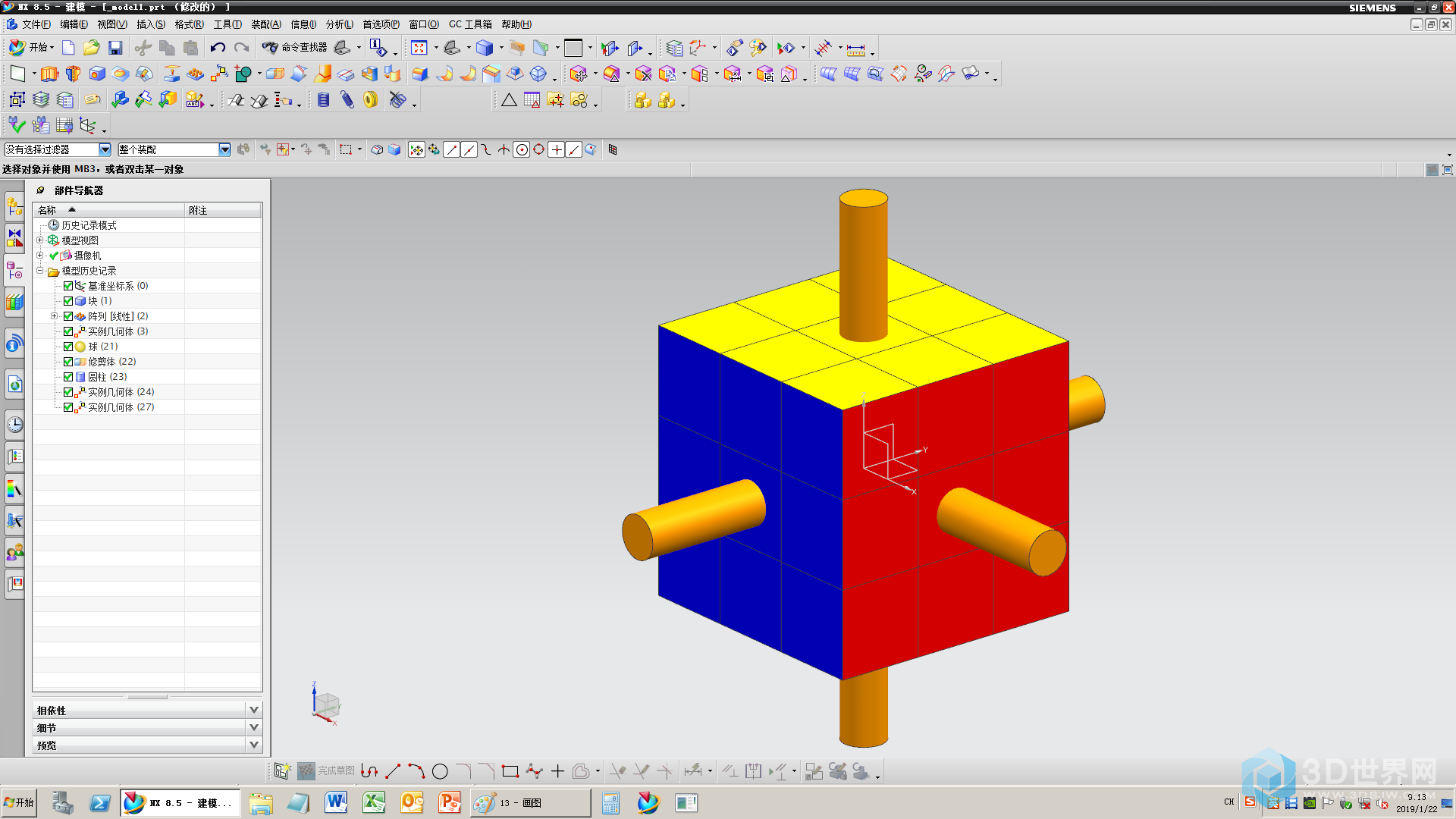
15、进入仿真模块
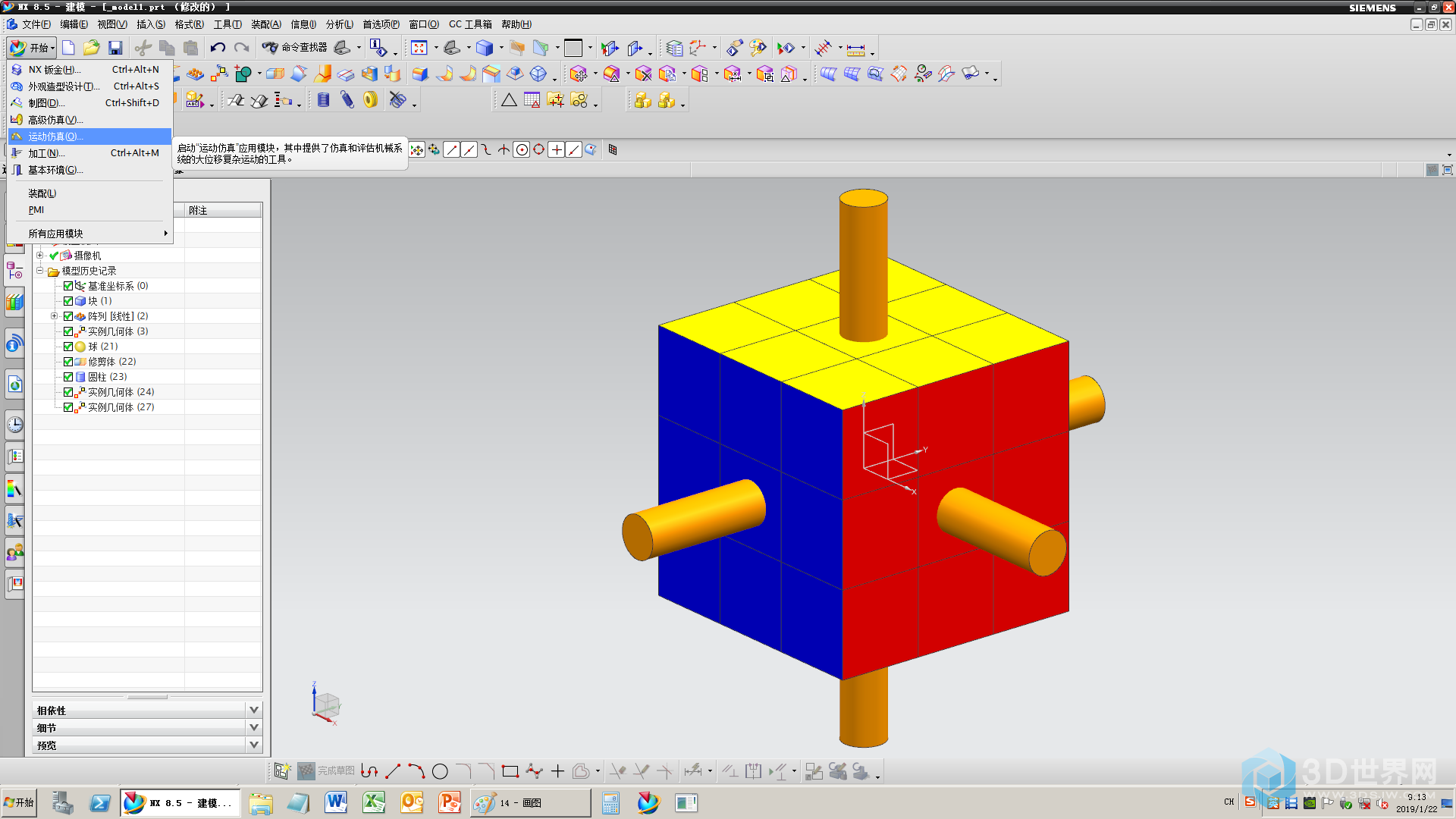
16、新建仿真
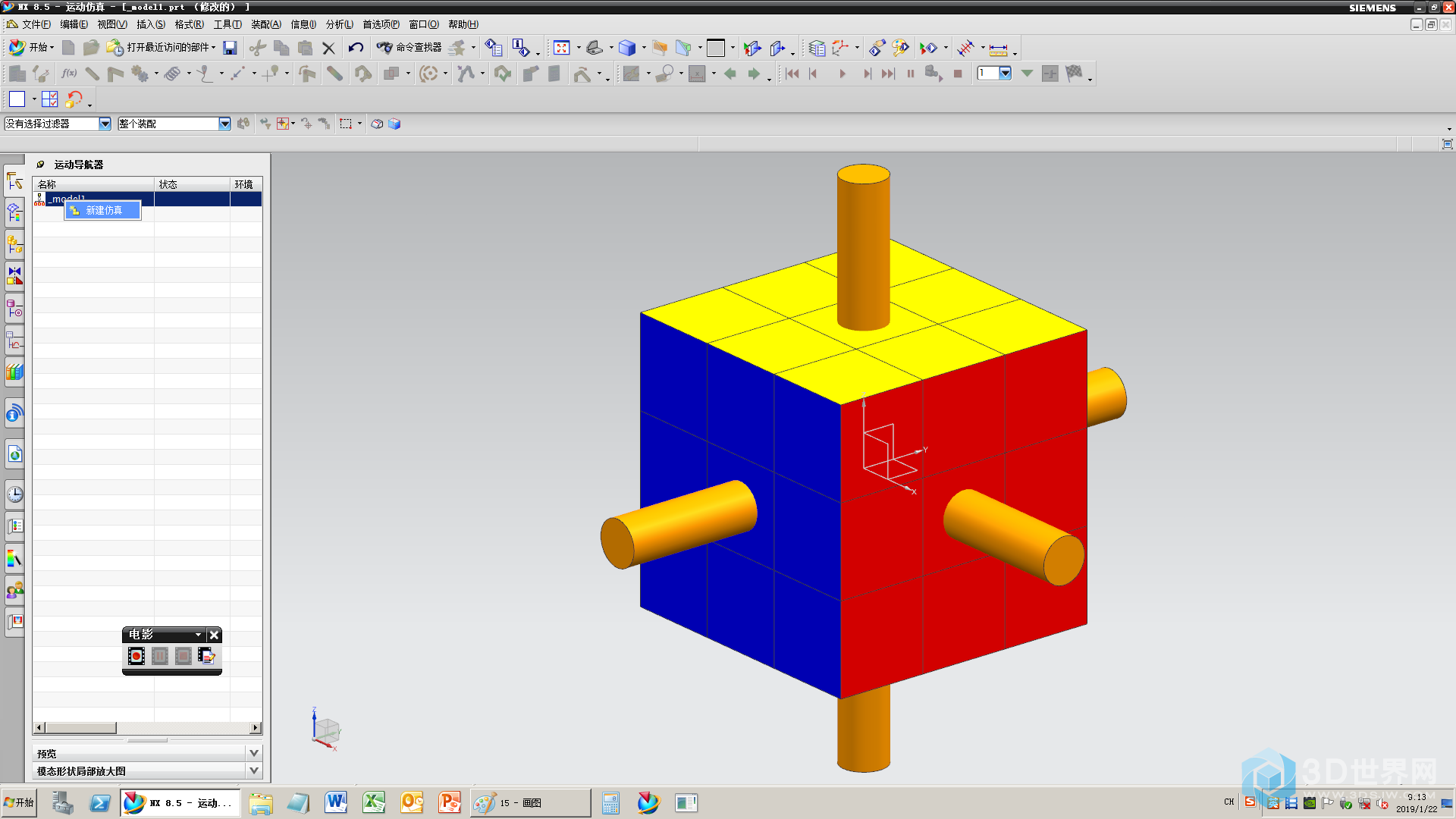
17、设定仿真环境
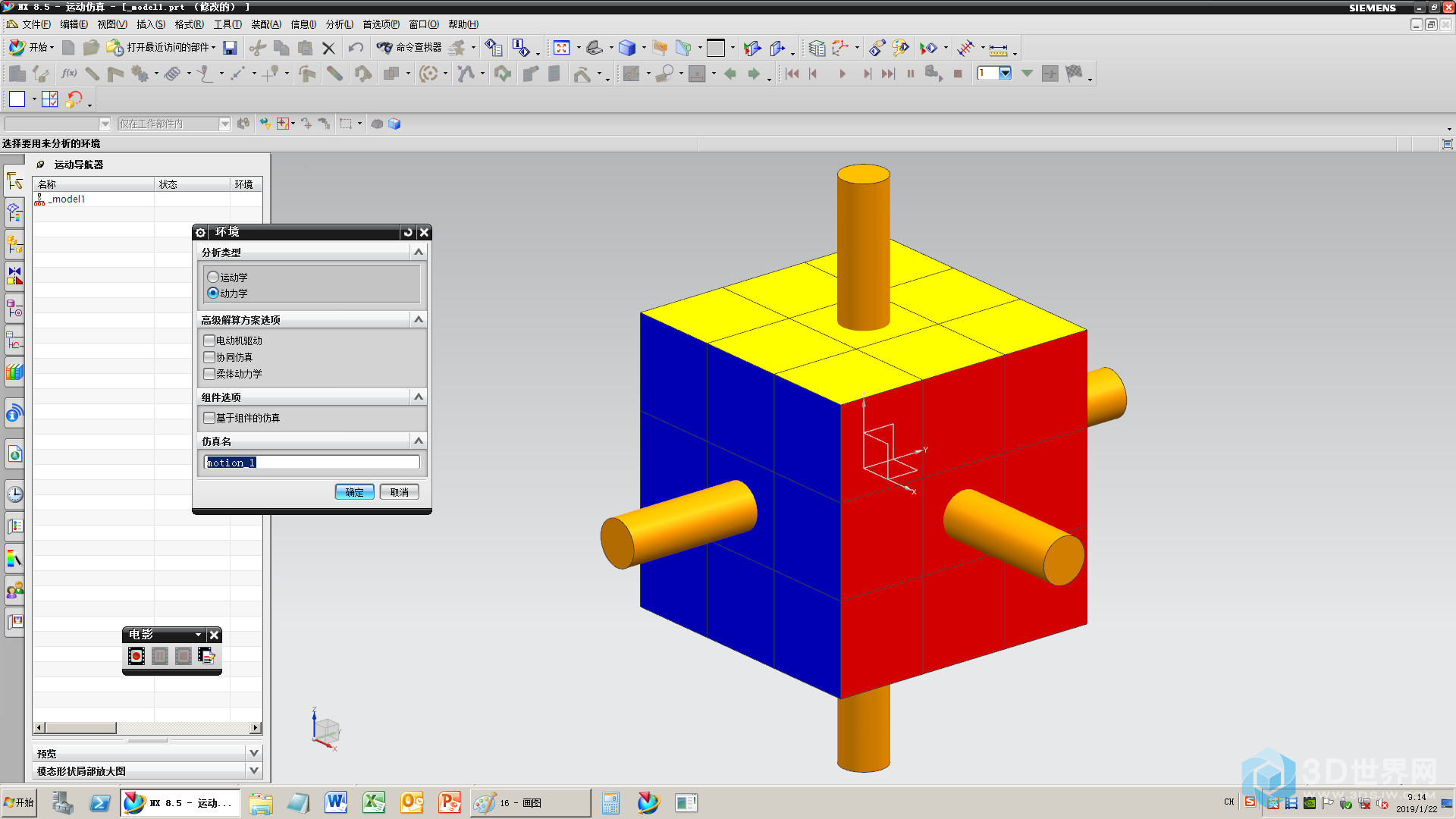
18、新建连杆(注意连杆规则)
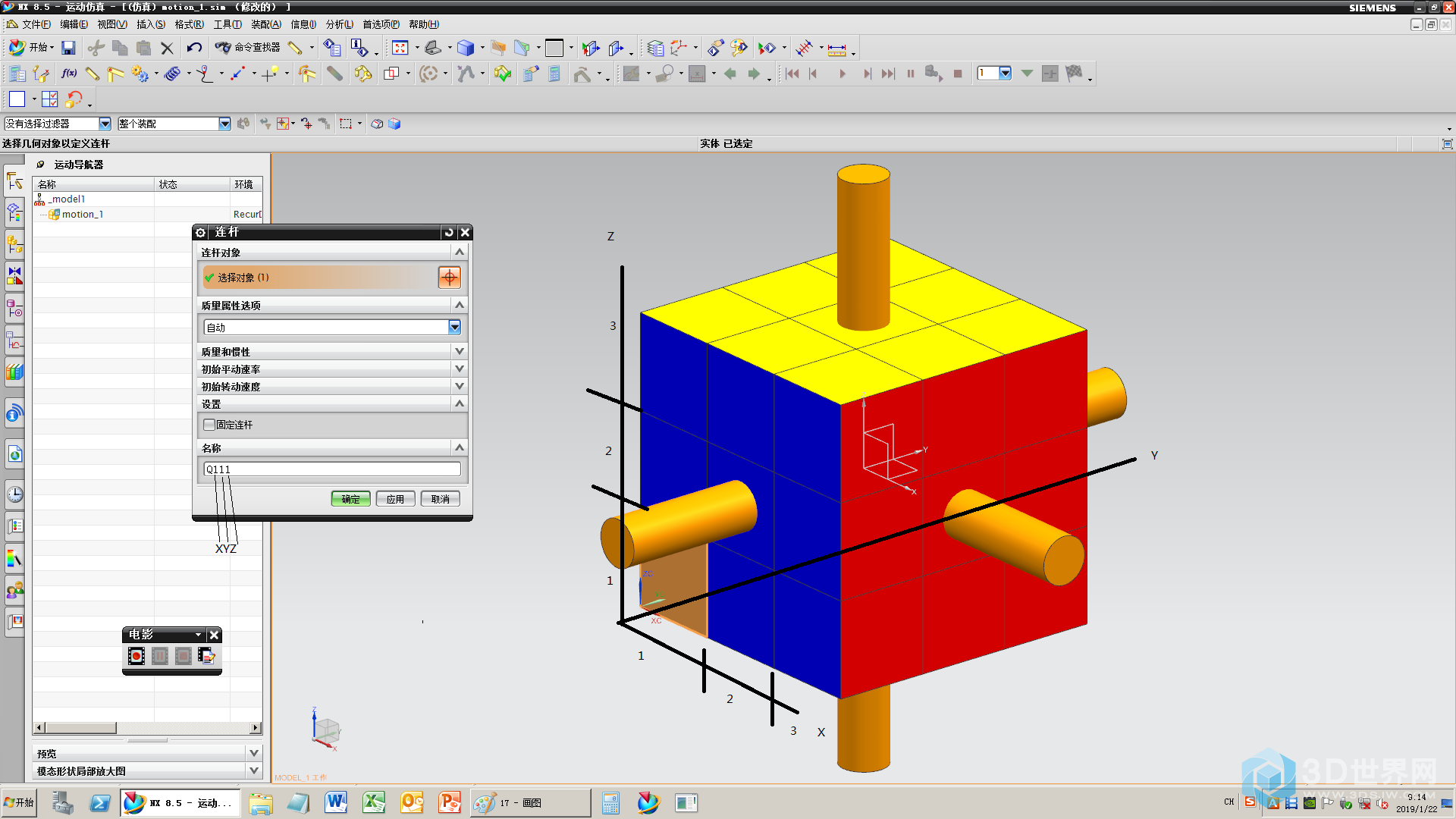
19、编号中带2个2的连杆(比如Q122、212、232等),轴要和方块作为1个连杆
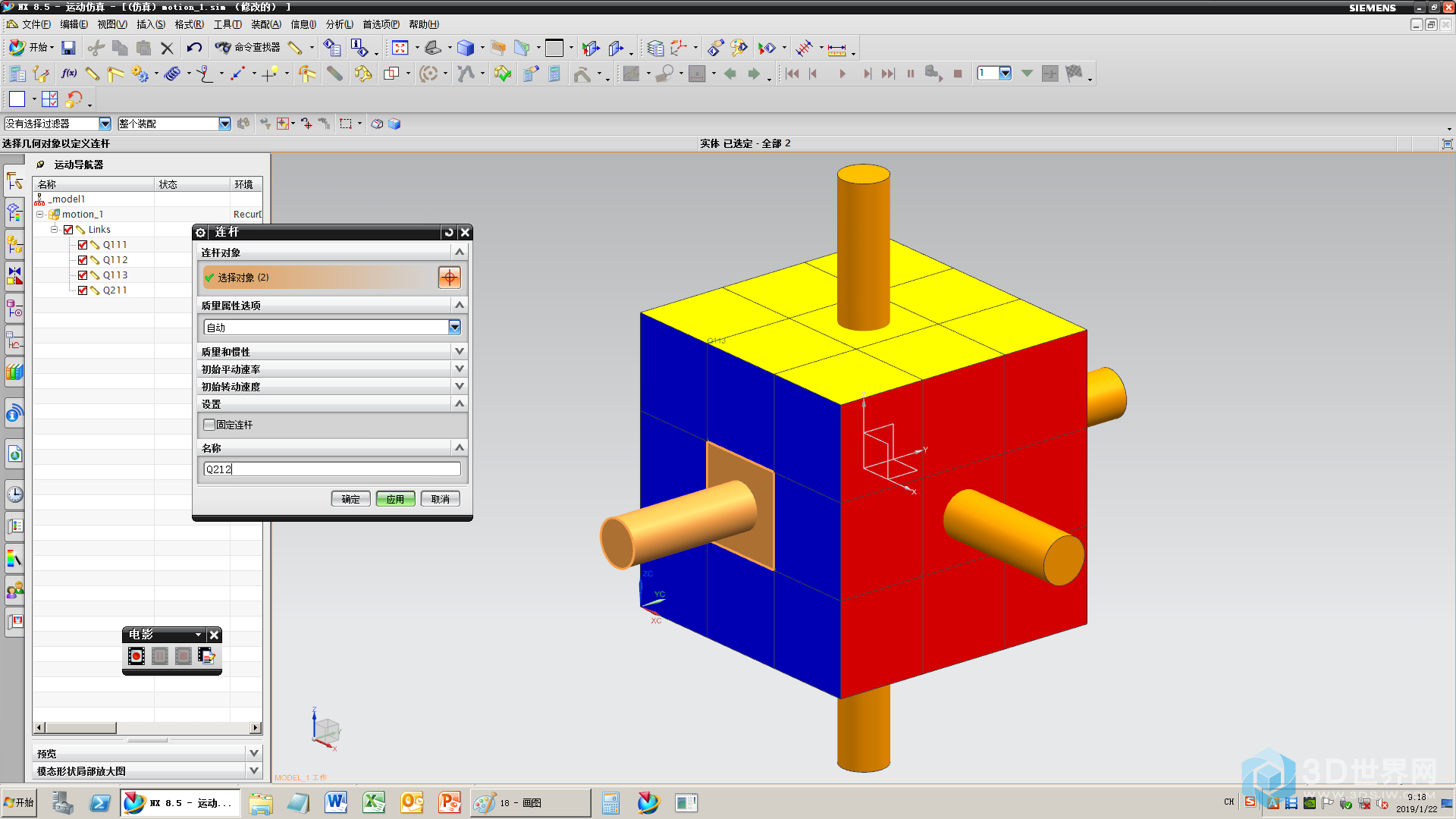
20、隐藏一层,定义下一层连杆(注意连杆规则)
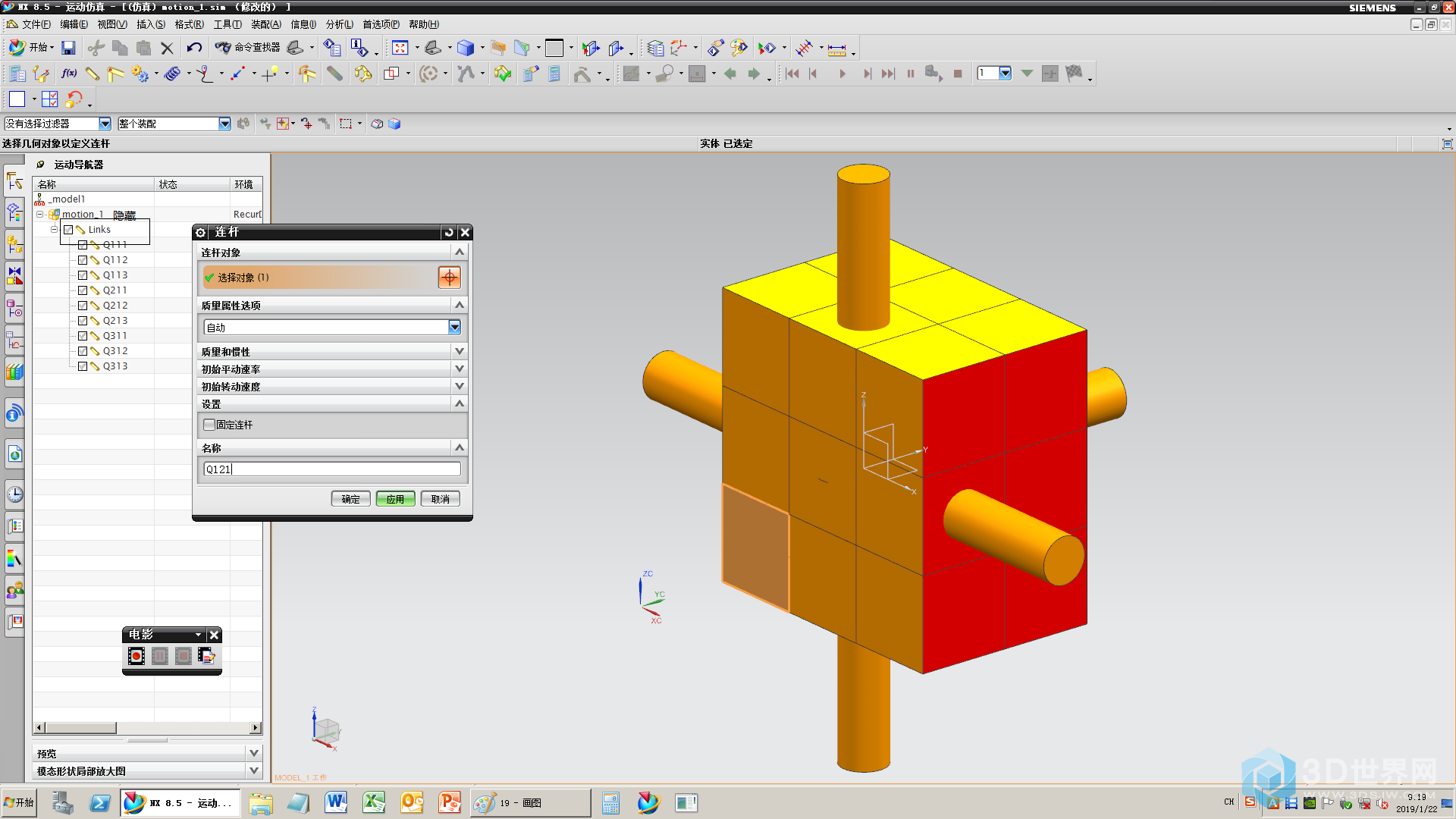
21、编号中带2个2的连杆(比如Q122、212、232等),轴要和方块作为1个连杆
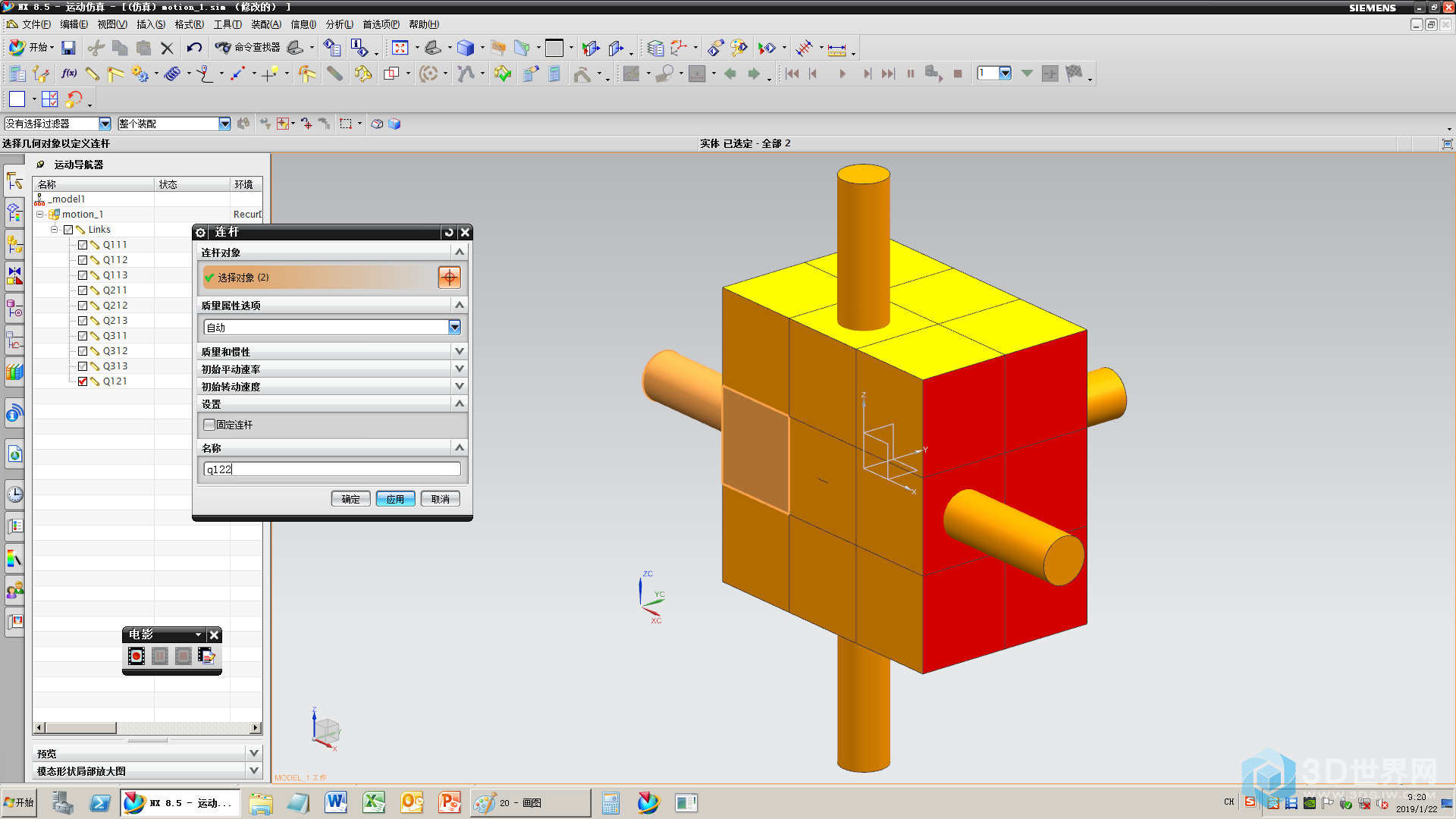
22、中央的方块不作为连杆
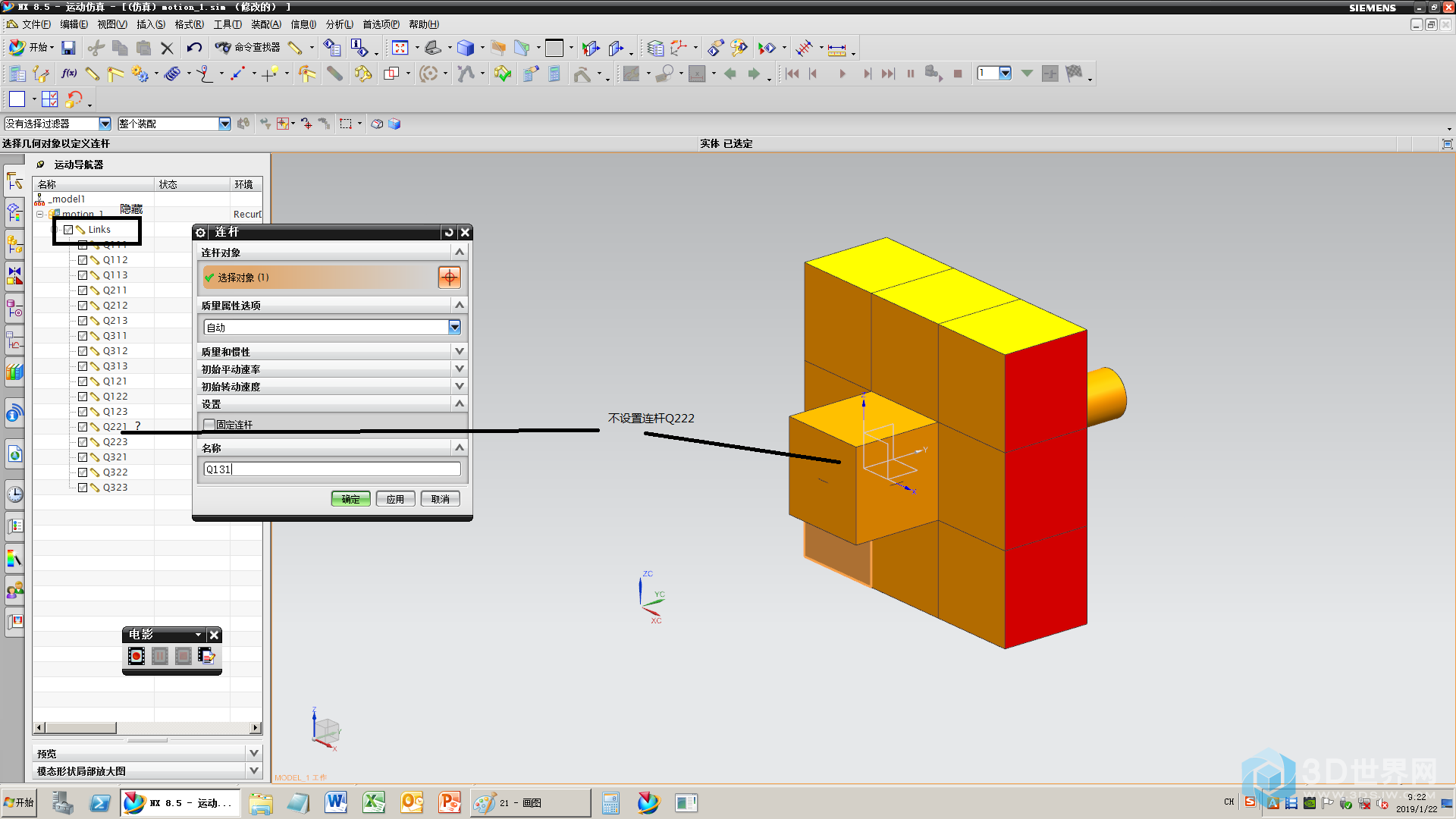
23、添加26个连杆后,将中央的方块隐藏
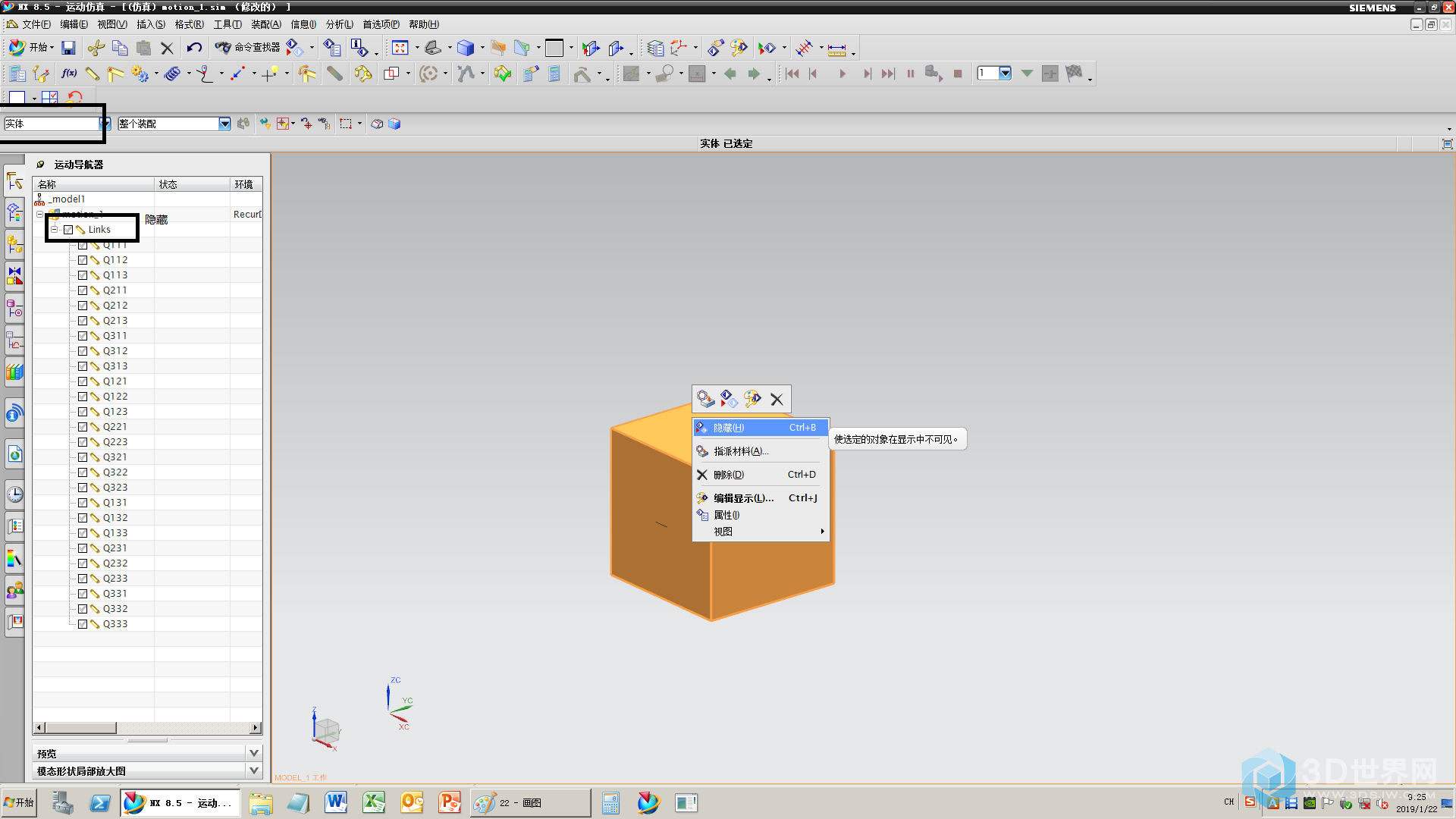
24、为中央的半球价格连杆
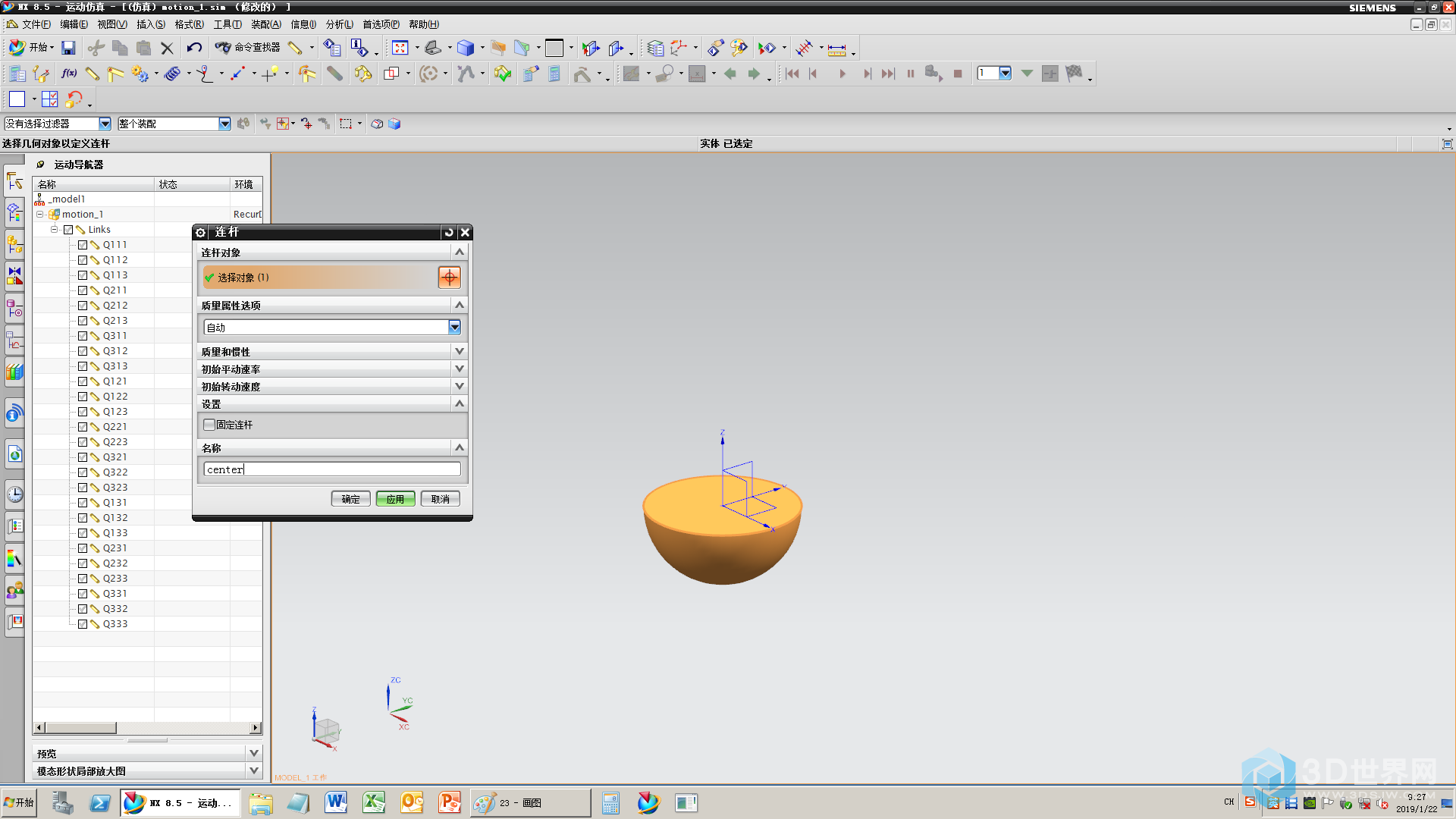
25、为方块和半球之间添加球面副,半球的好处就体现出来了,可以选圆边,如果是圆球的画,还要选圆心
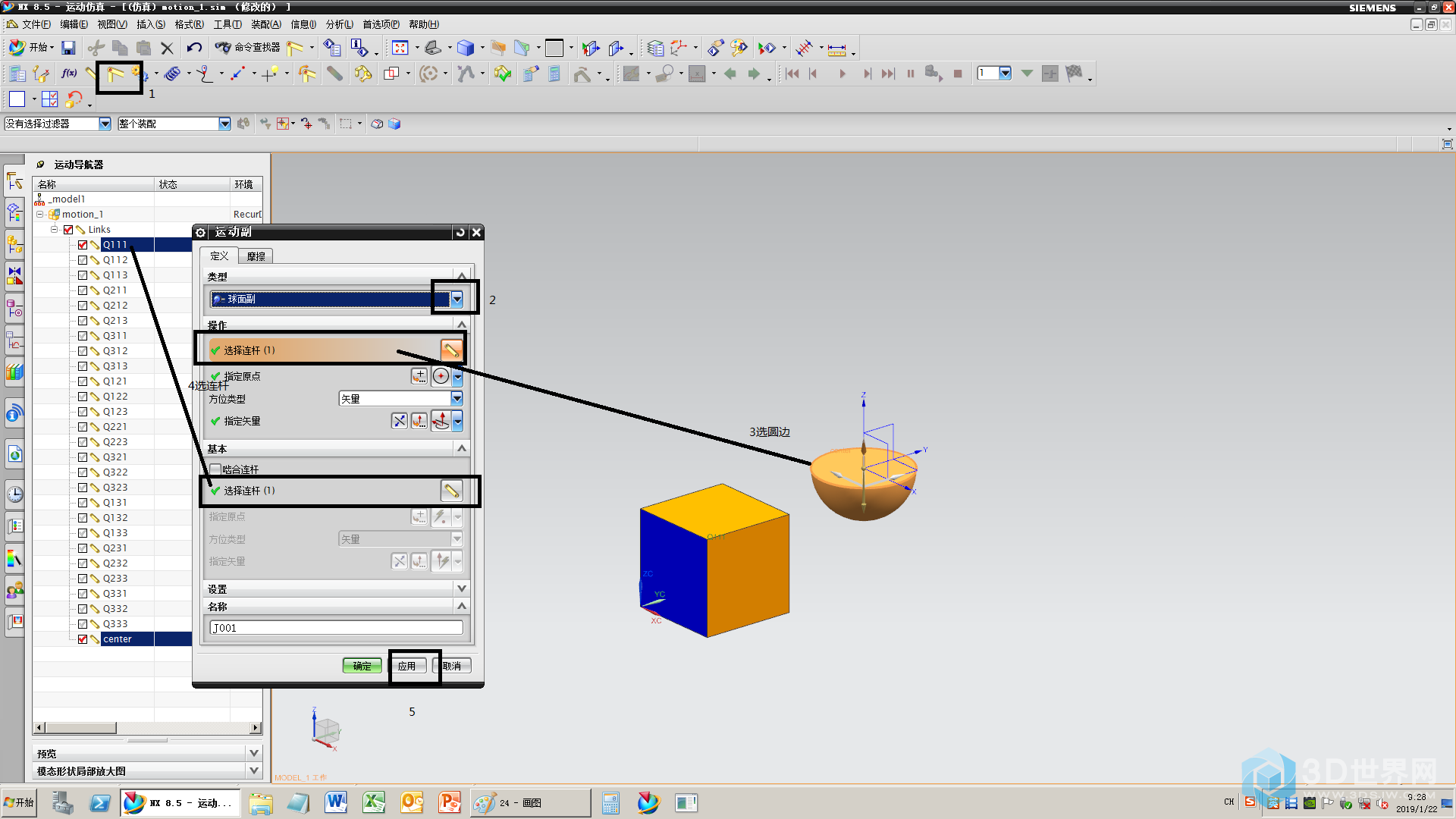
26、添加26个球面副
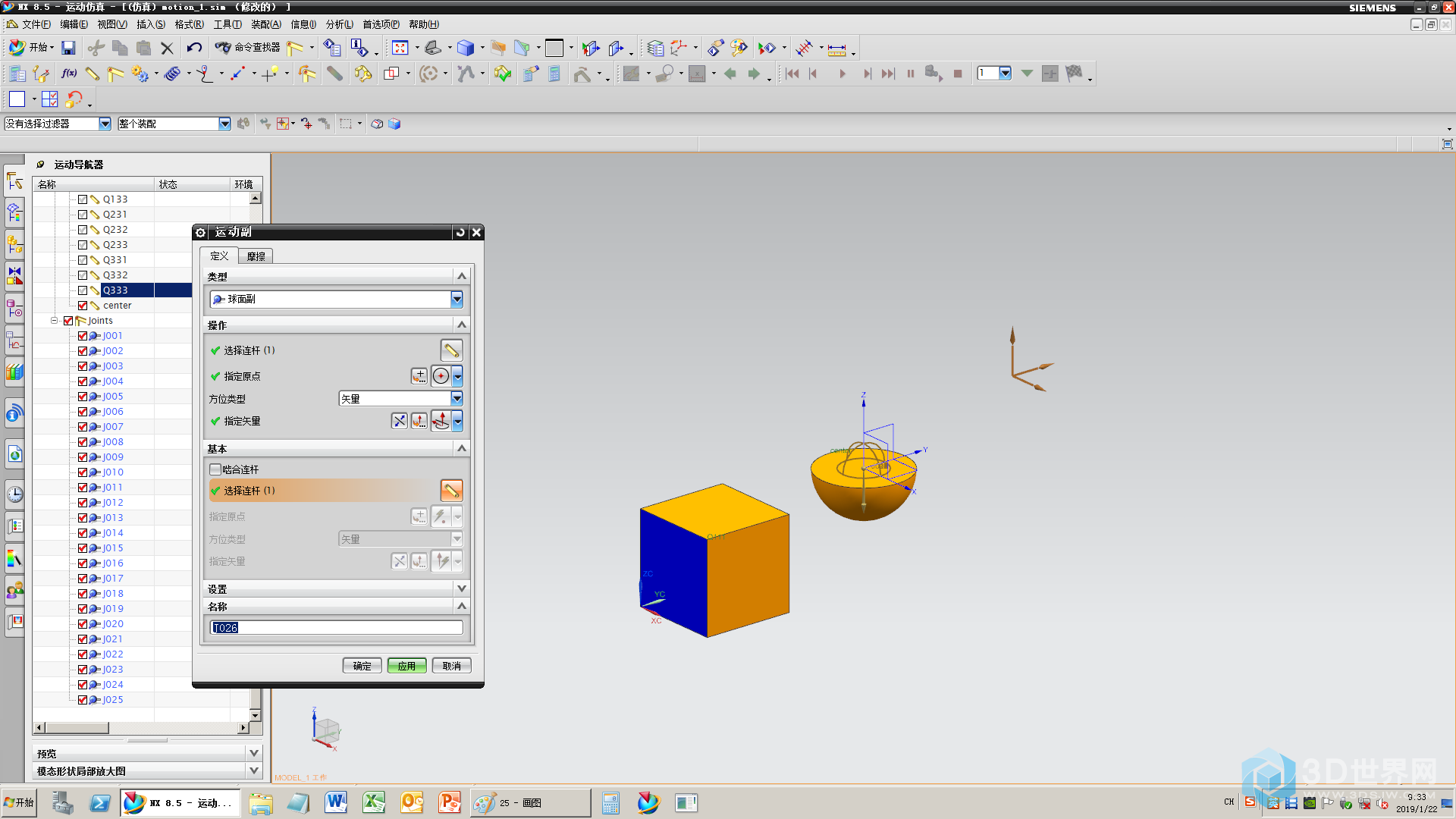
27、给半球加固定
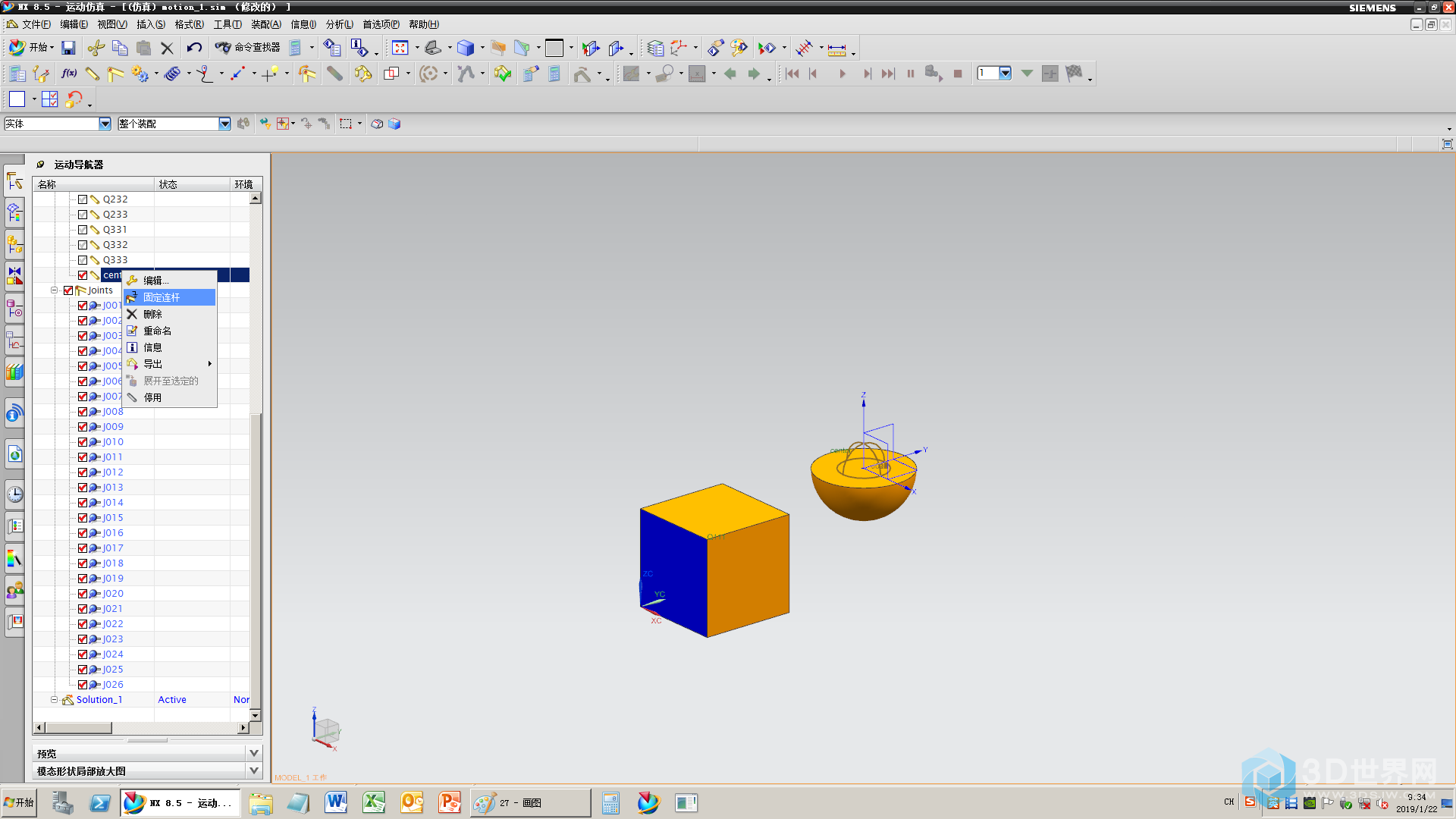
28、新建个解算方案
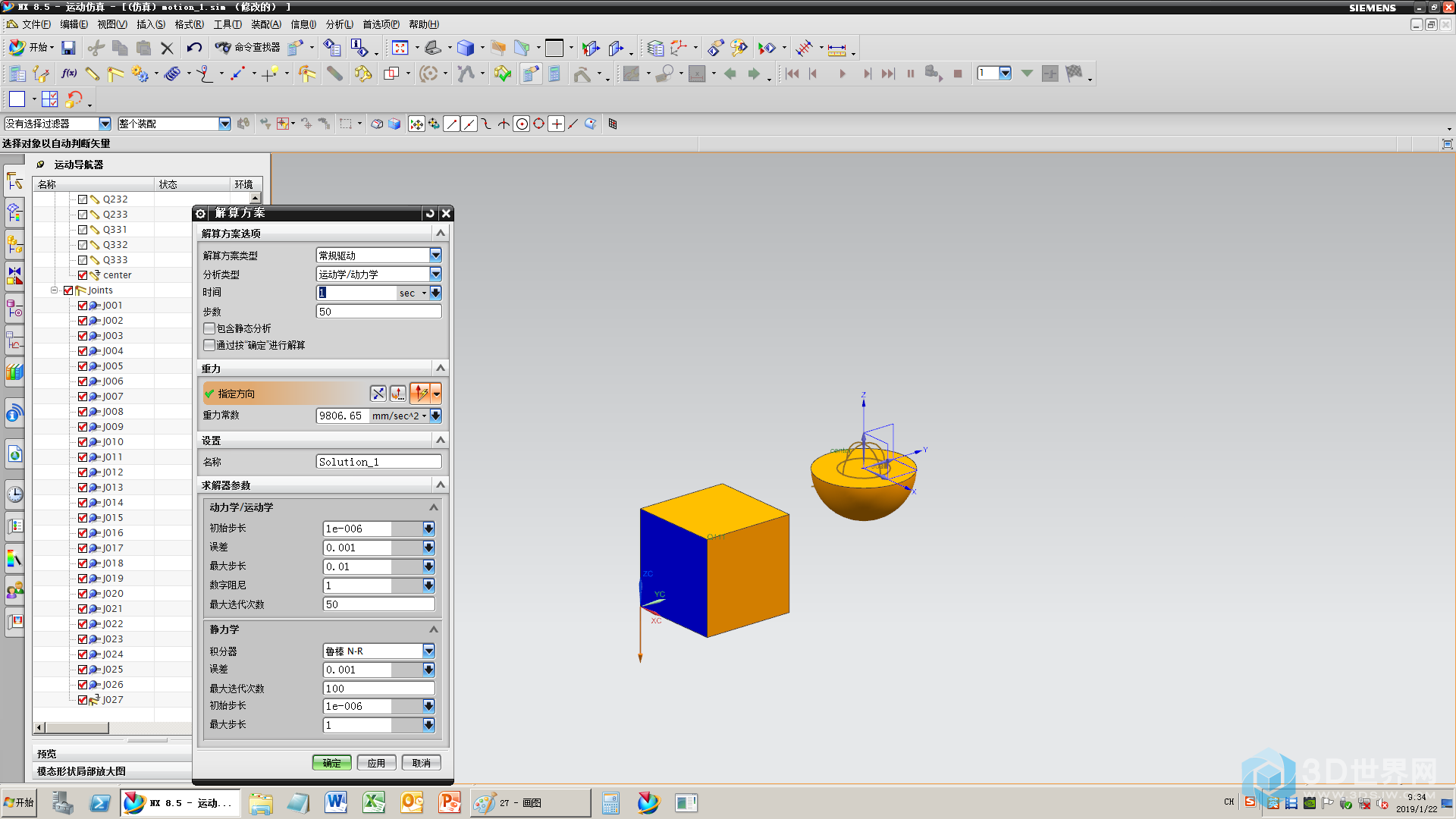
29、求解查一下错,一切正常
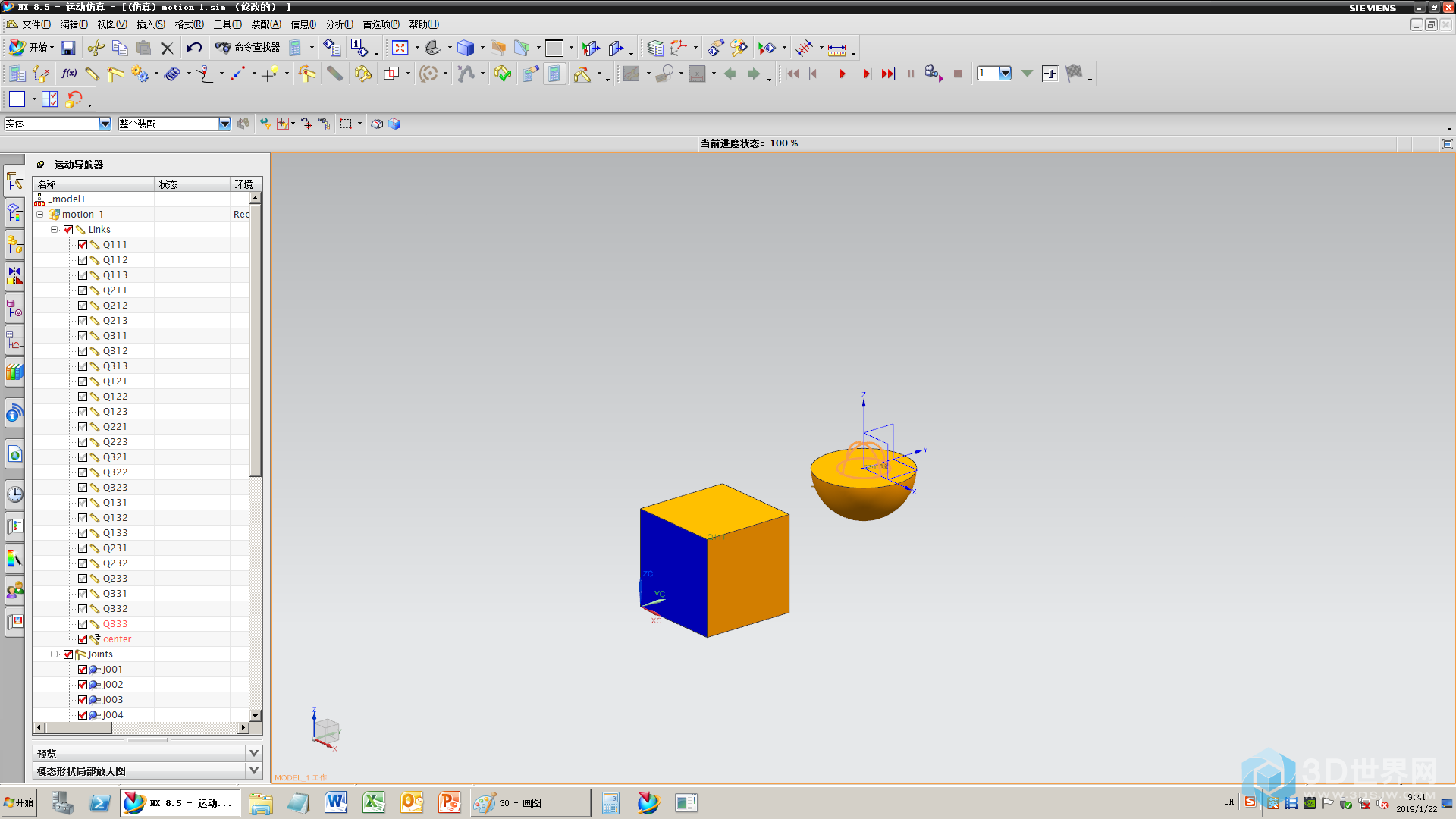
30、播放查一下错,一切正常
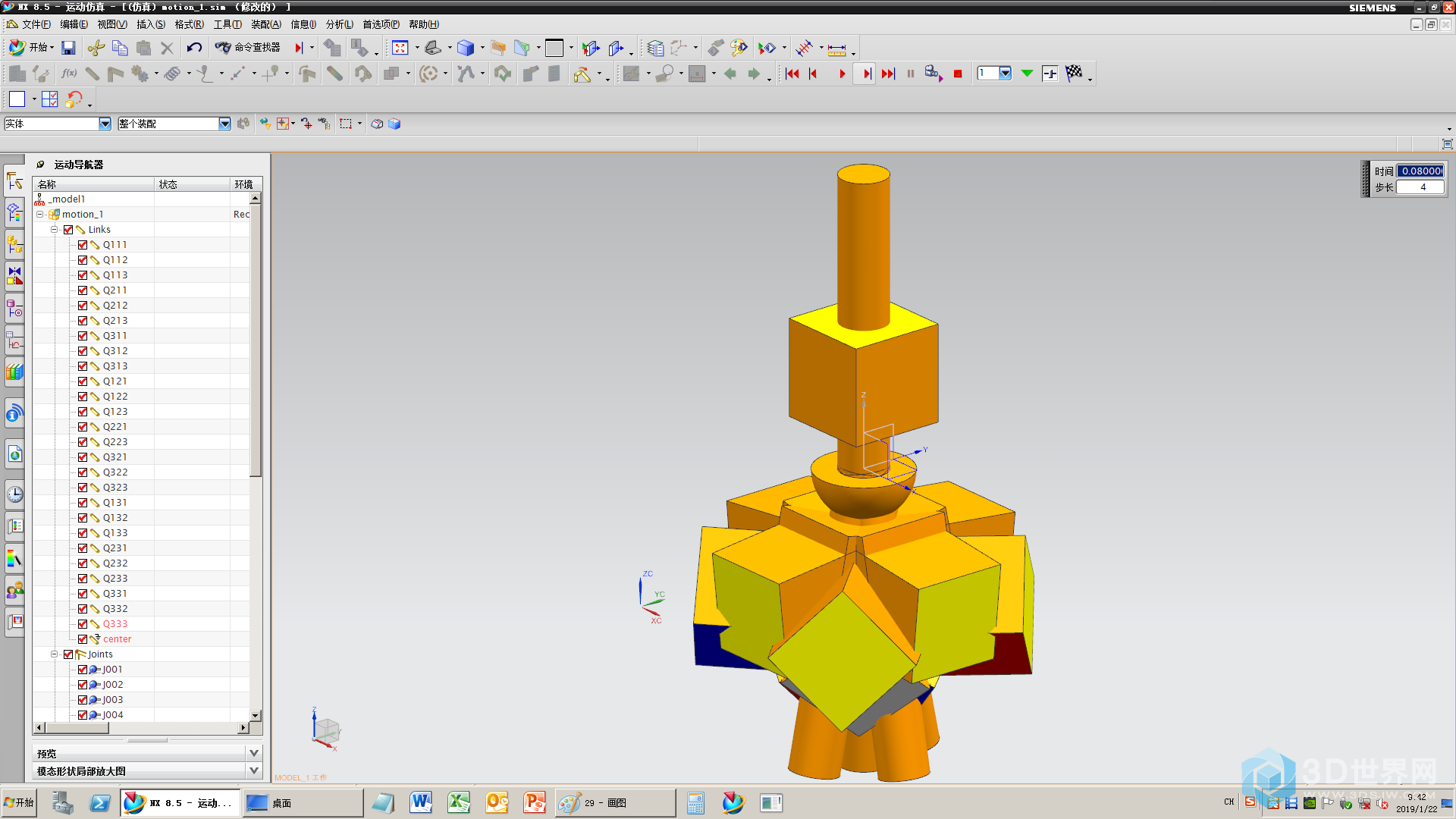
31、添加轴的旋转副
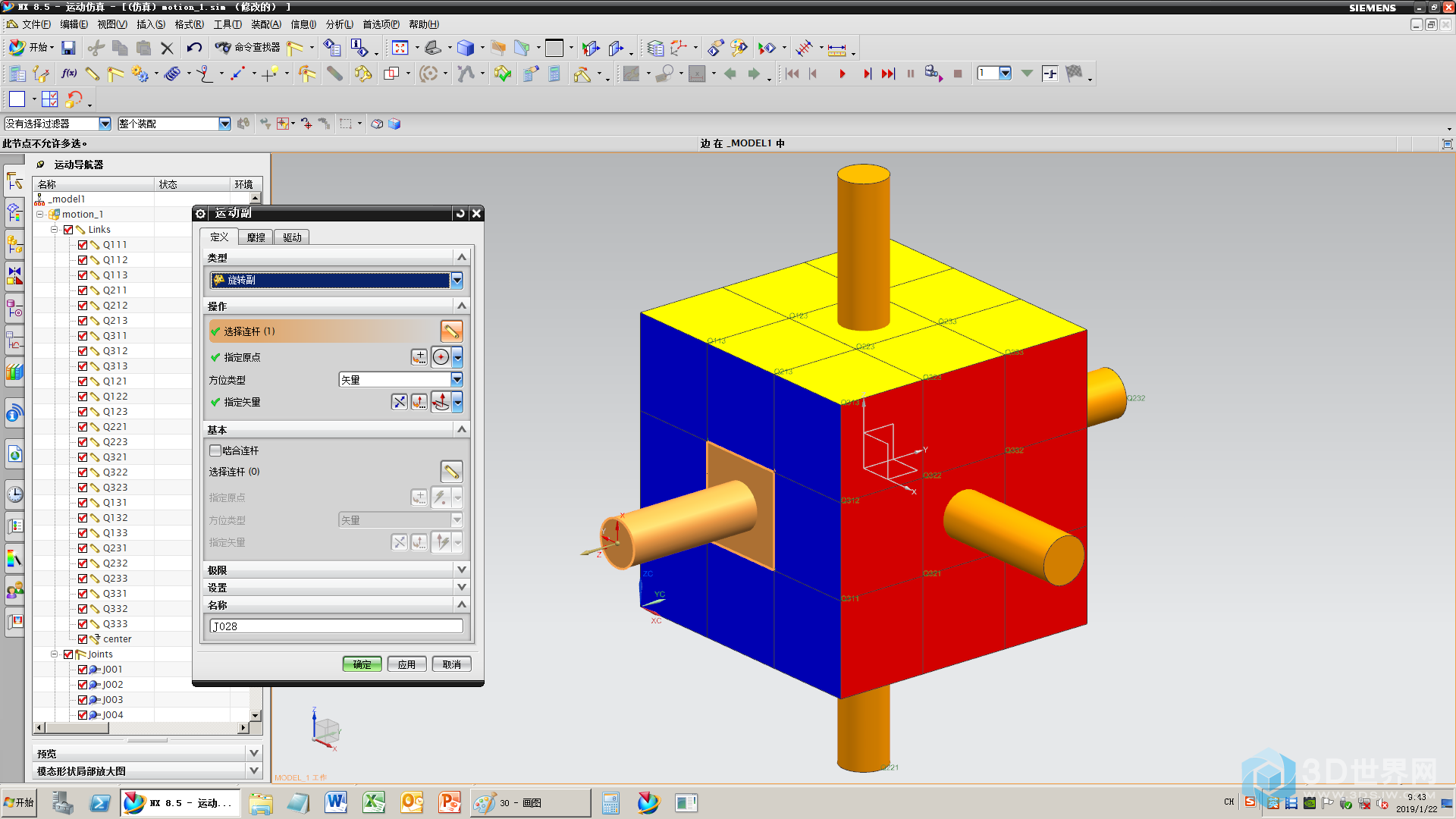
32、添加6个旋转副
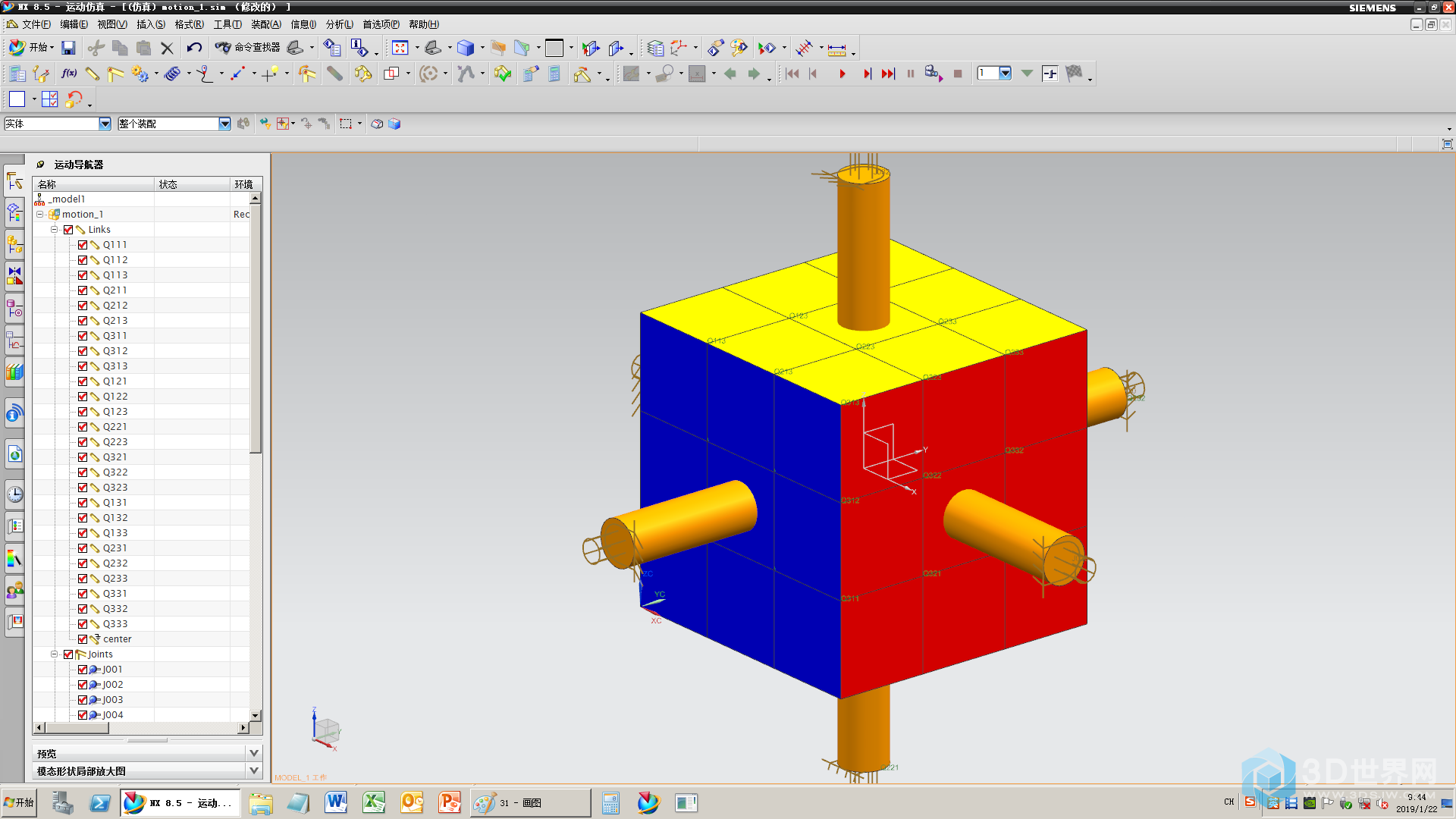
33、求解查错,有冗余项5、16、22、11、14、15
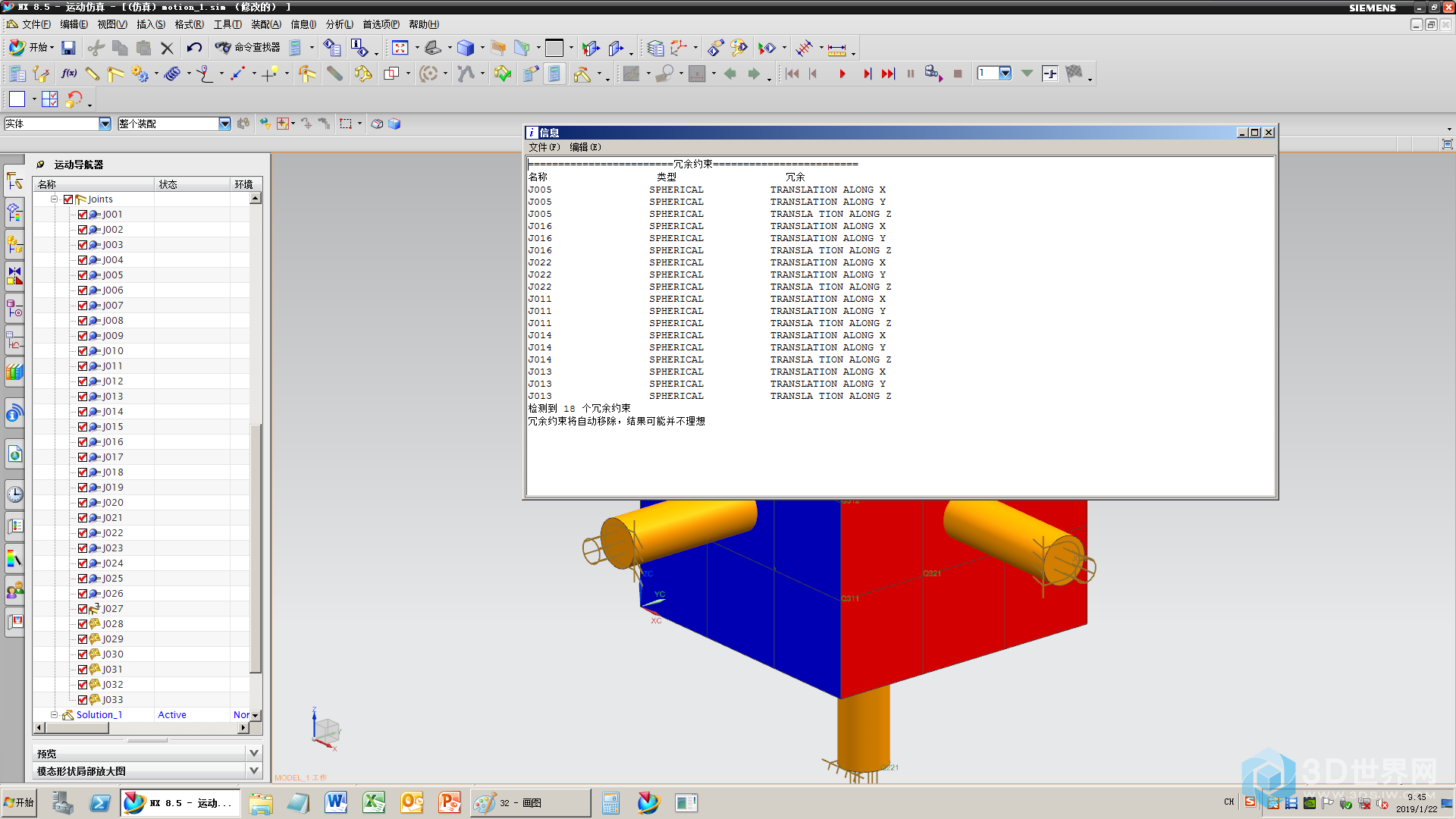
34、选中5、16、22、11、14、15,停用
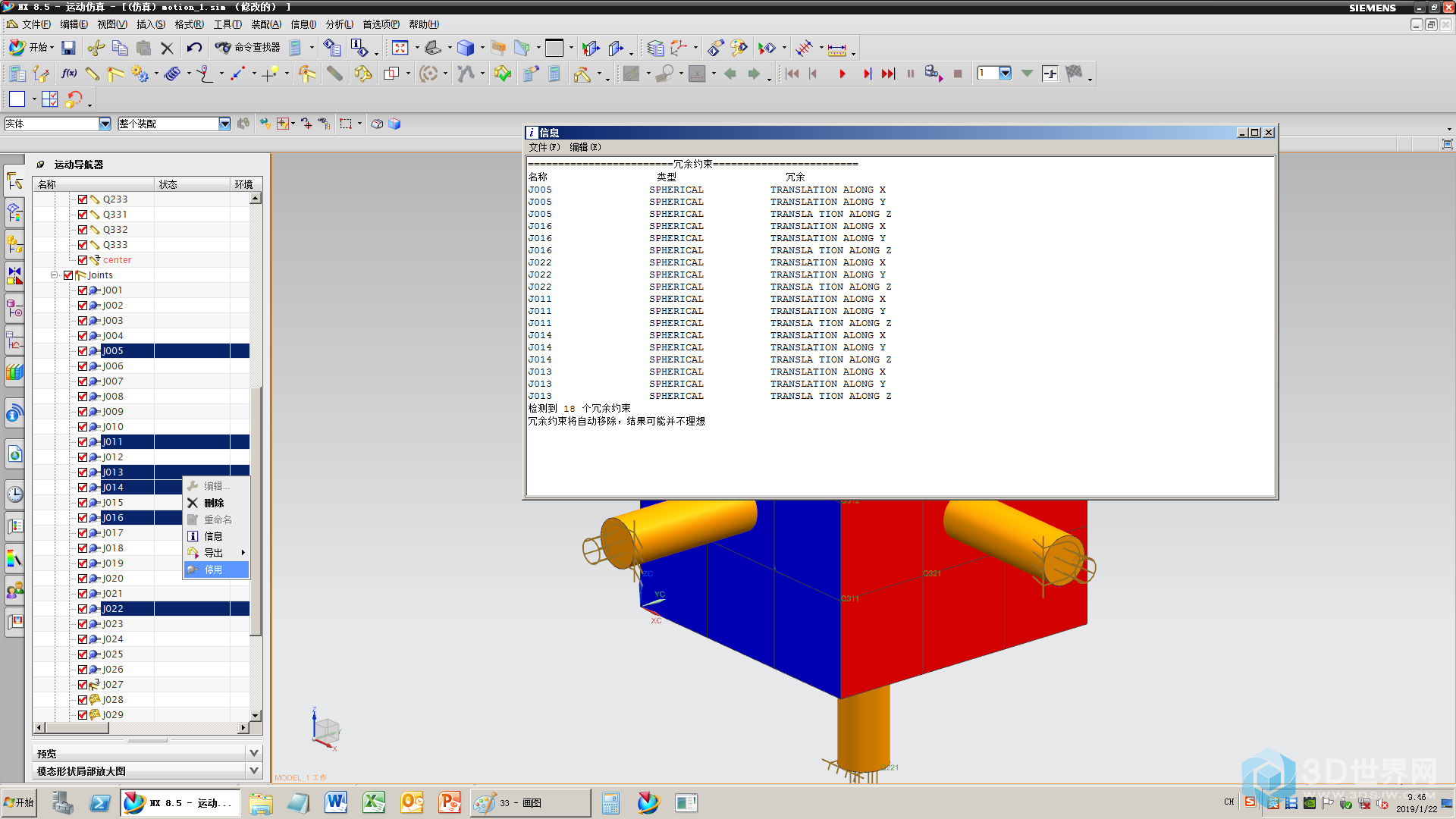
35、求解查错,一切正常

36、播放查错,一切正常
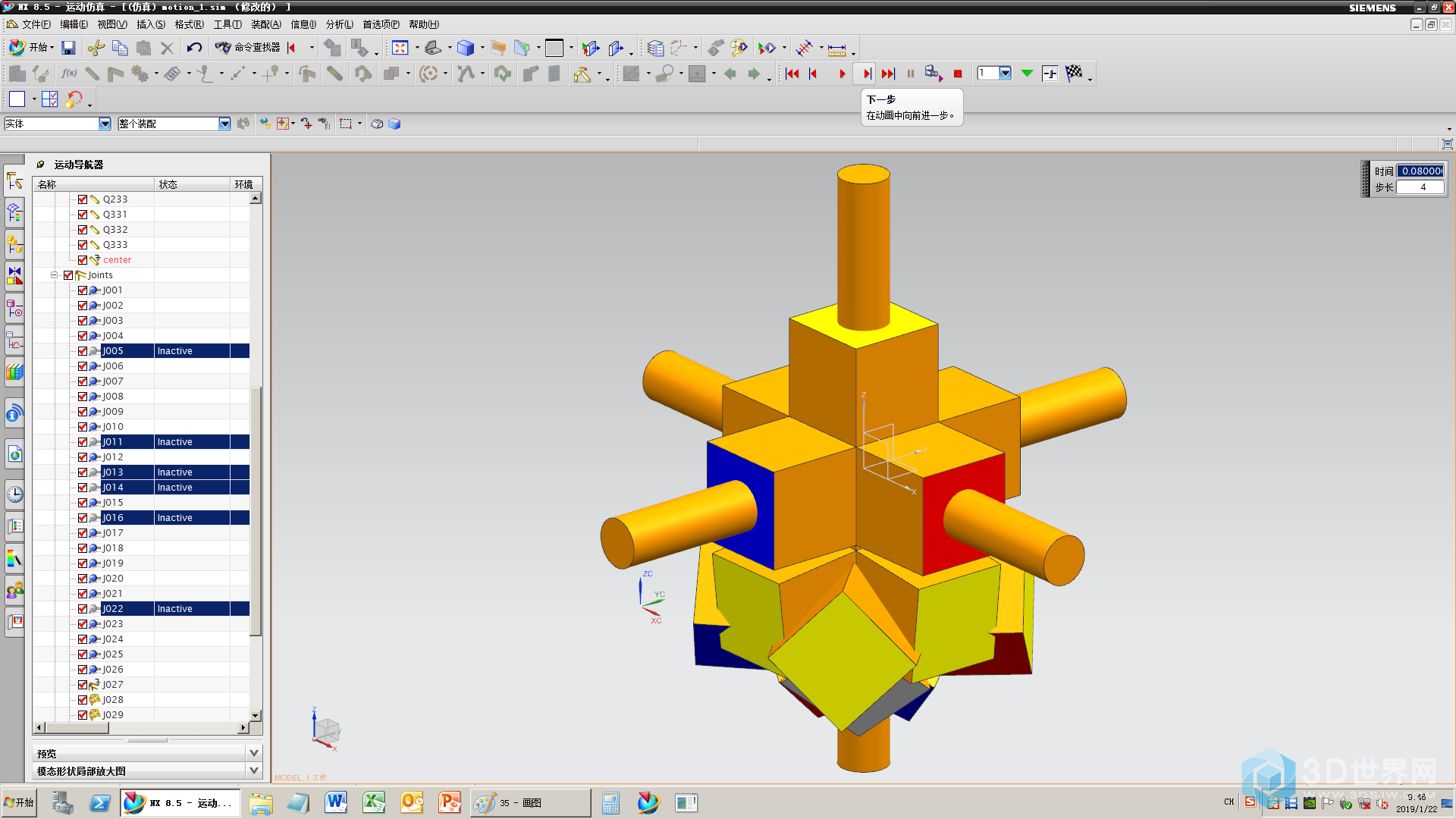
37、添加碰撞(“轴链接的方块”和12个“十字线上的方块”之间的12个碰撞)
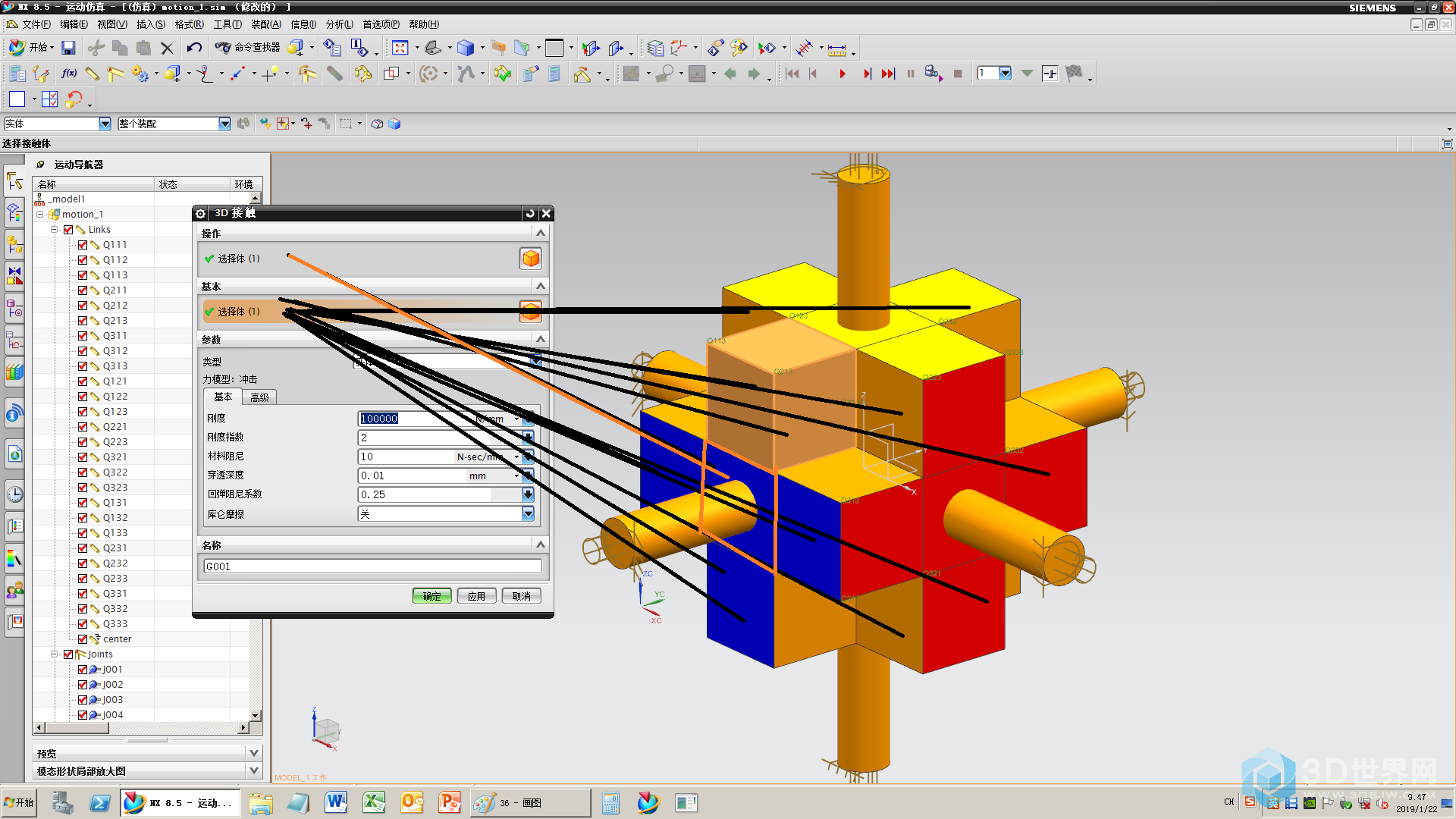
38、添加72个碰撞
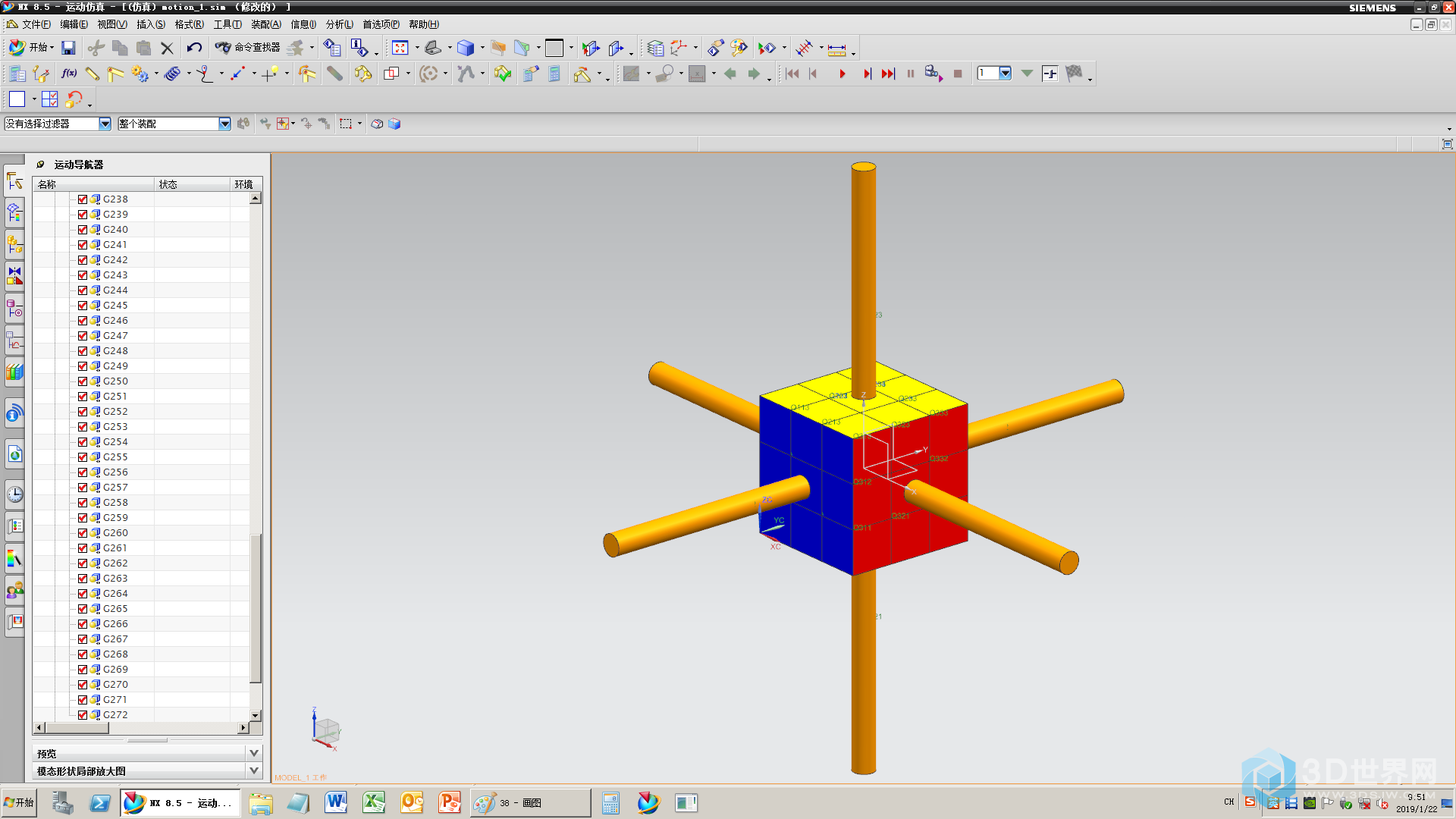
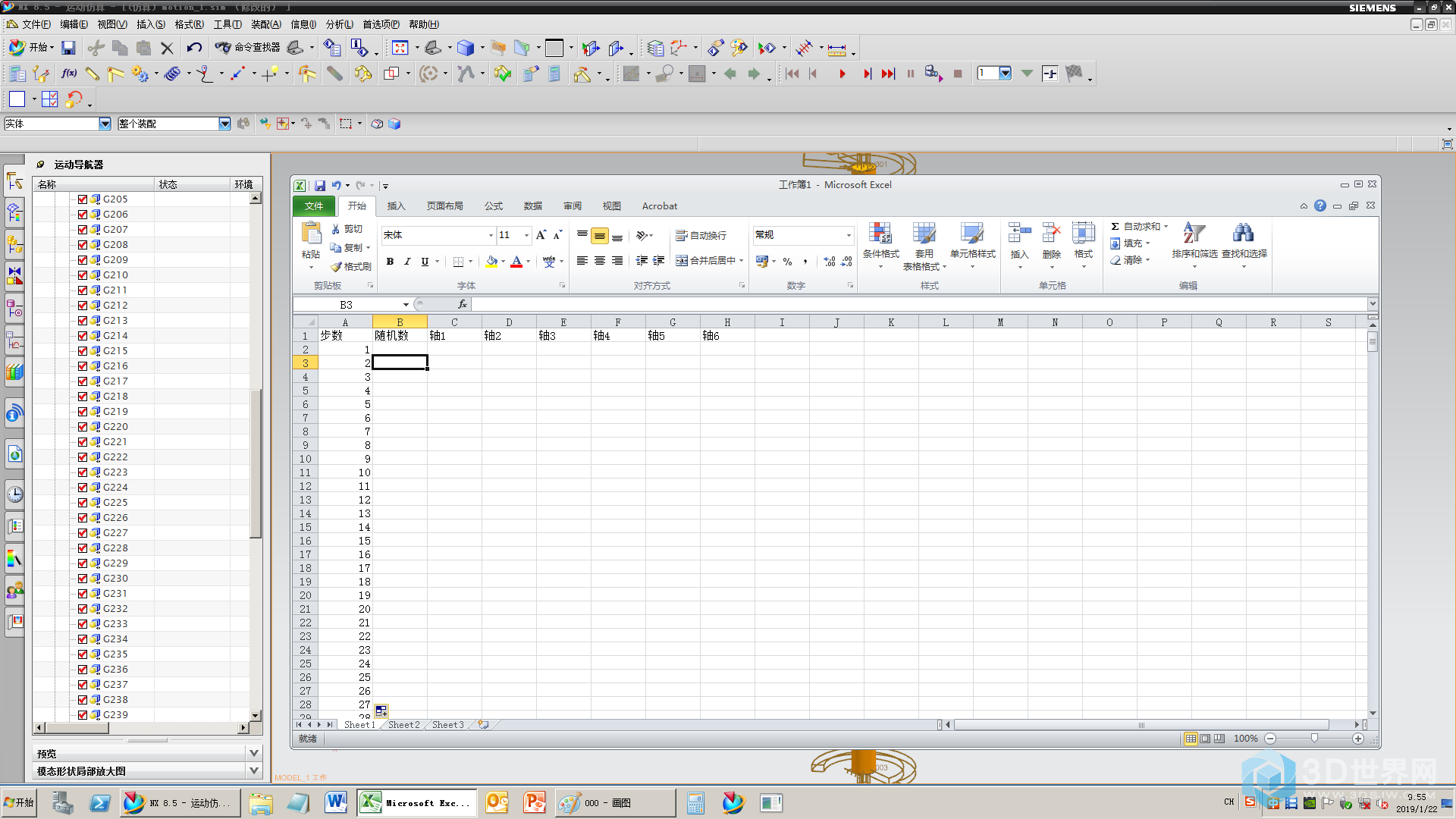
39、新建excel表,500步,通过随机数来确定1~6号轴哪根轴转动
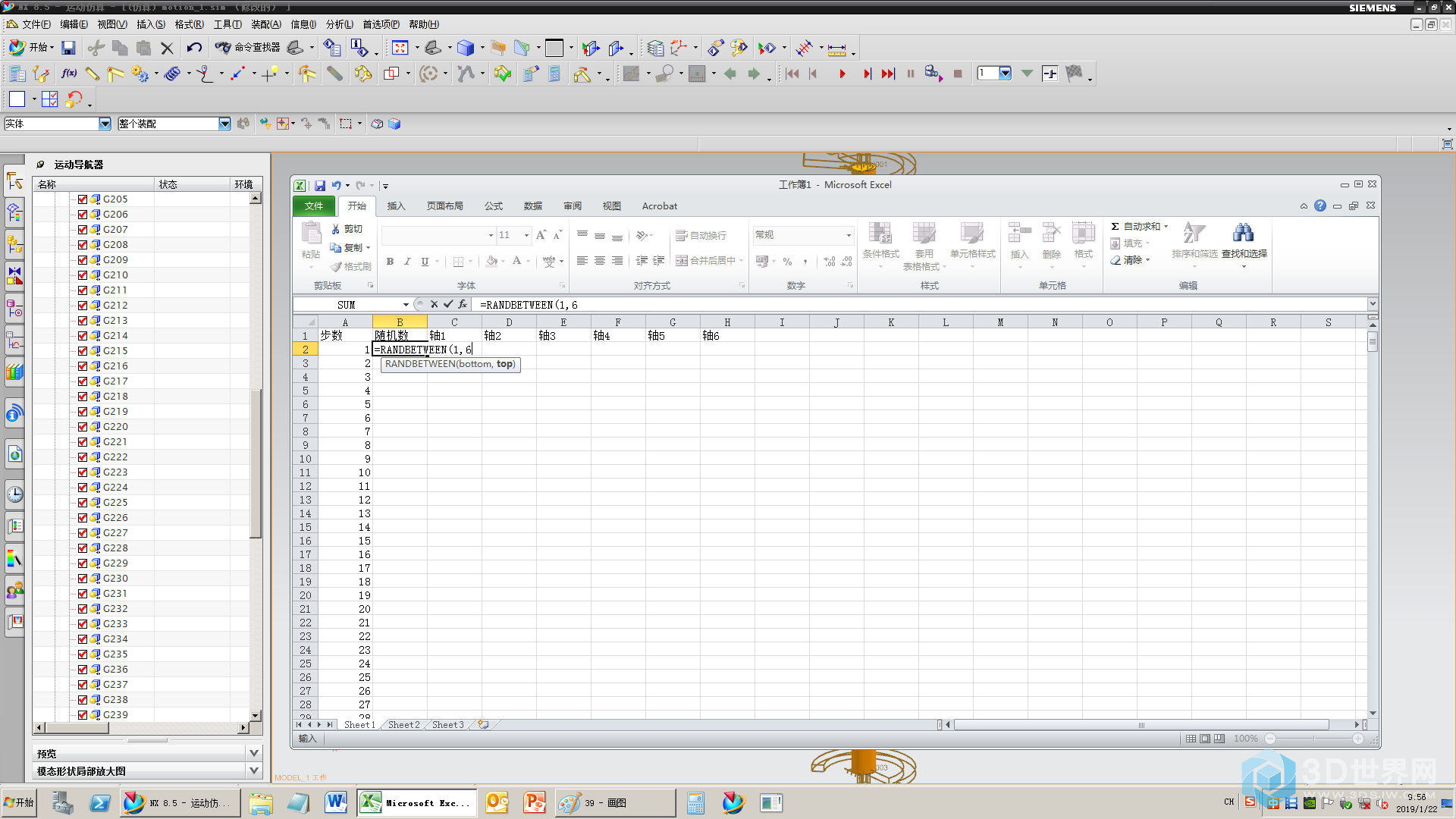
40、定义一个1~6的随机数=randbetween(1,6)
41、填充
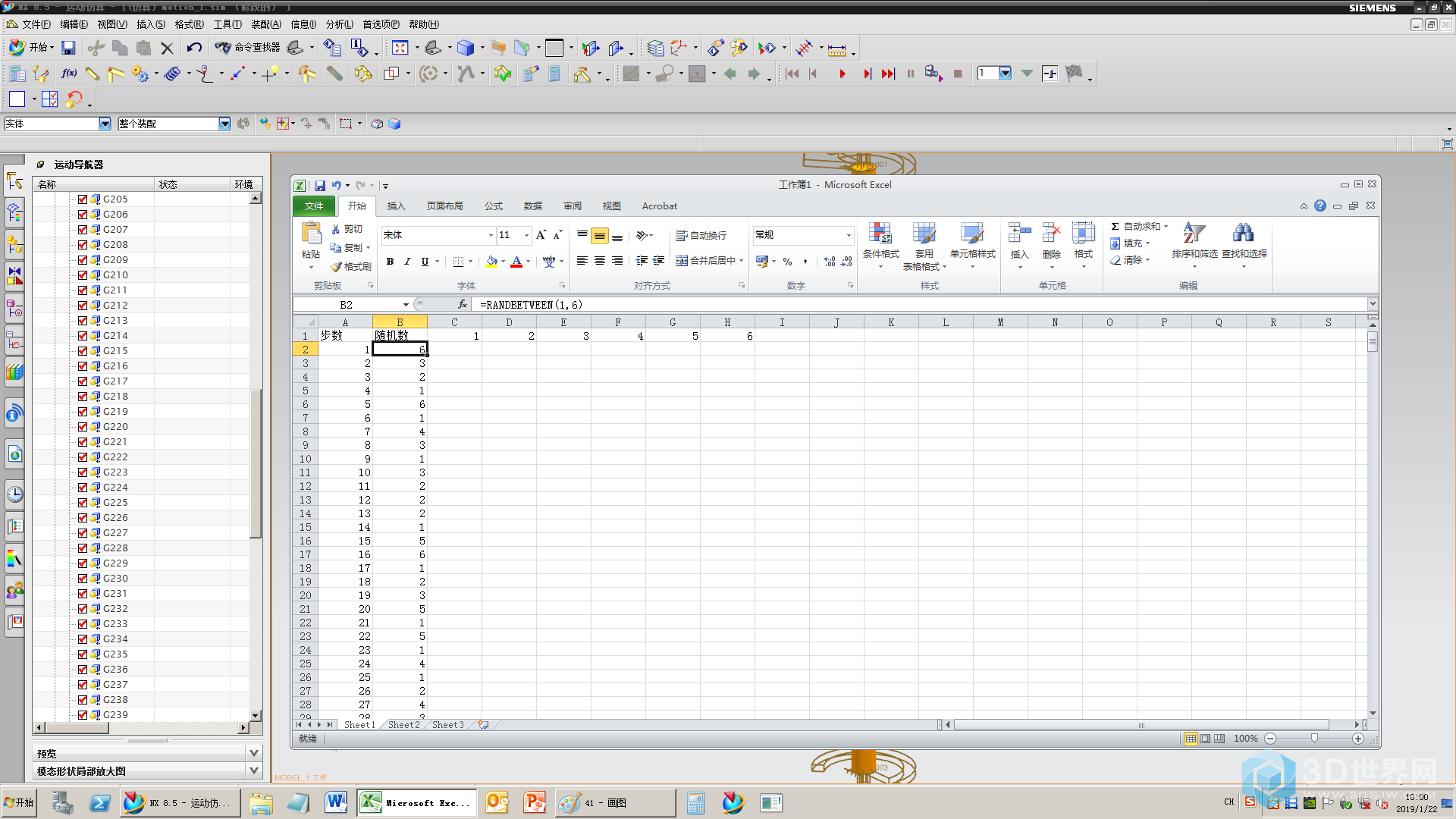
42、
C2输入函数=if($B2=C$1,90,0)如果随机数等于C1,转90度,否则转0度,填充
C3输入函数=C2+if($B3=C$1,90,0)如果随机数等于C1,在上一步的基础上转90度,否则不转,填充
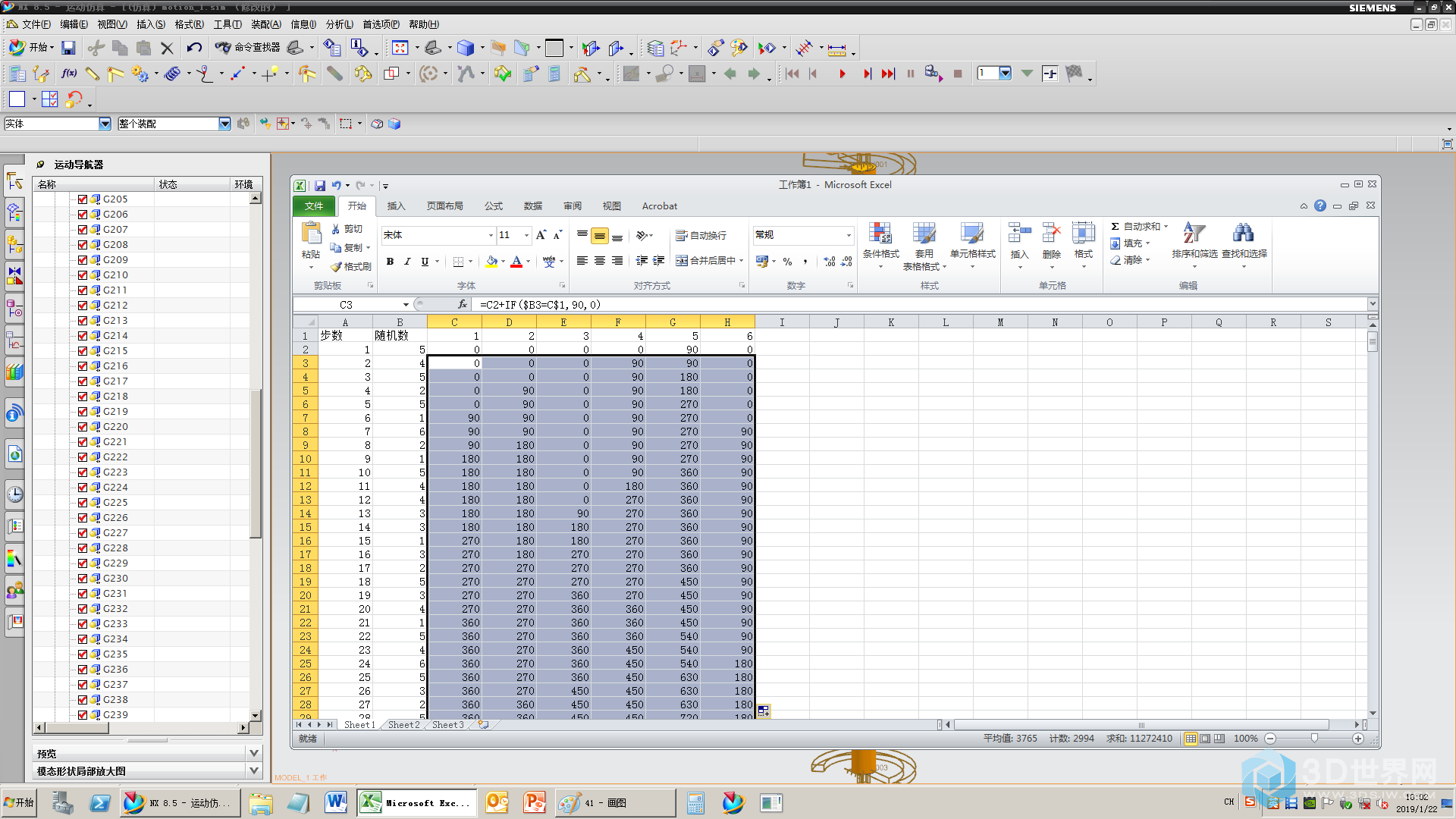
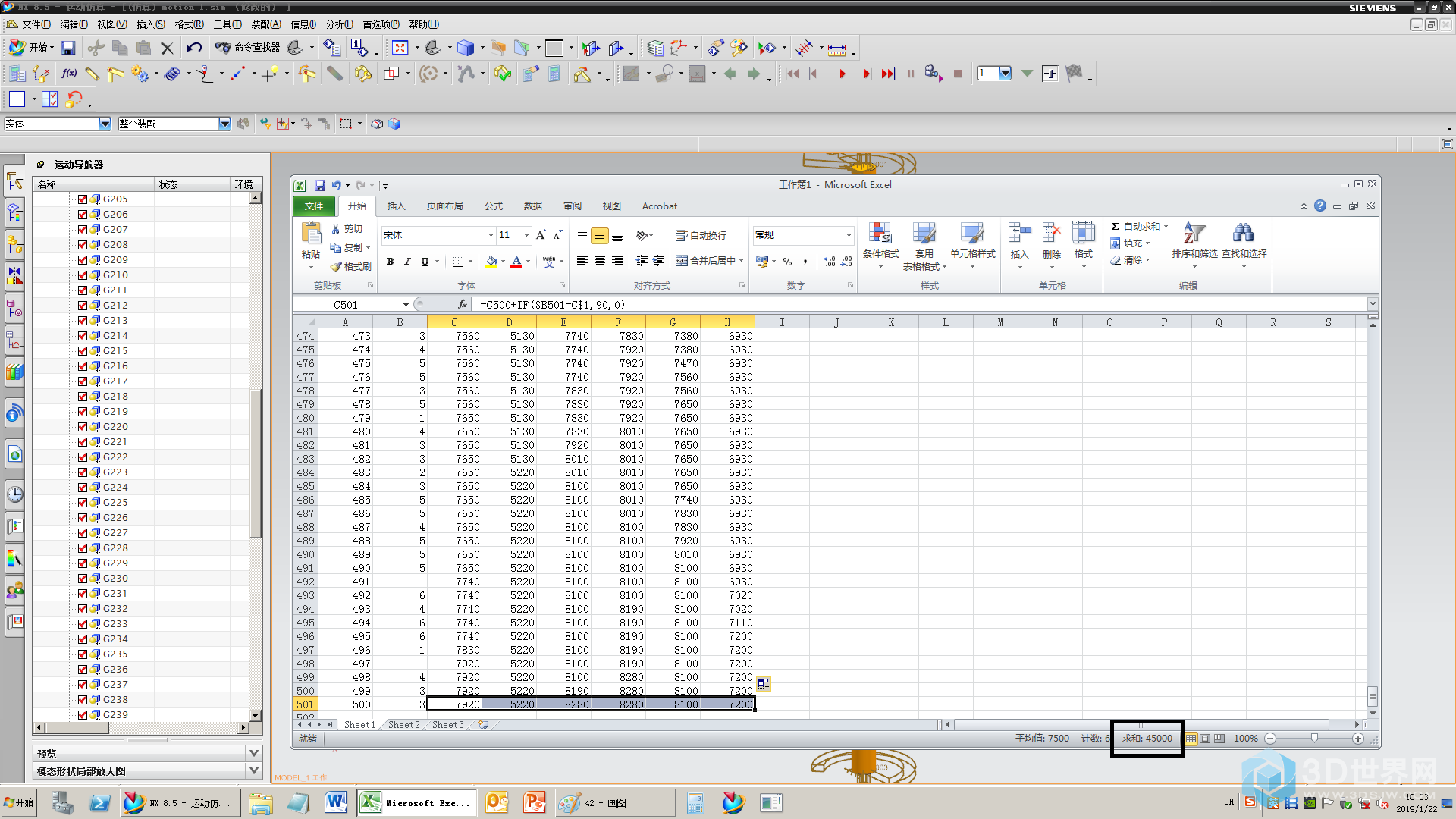
43、翻到最后一行求和查错,一切正常
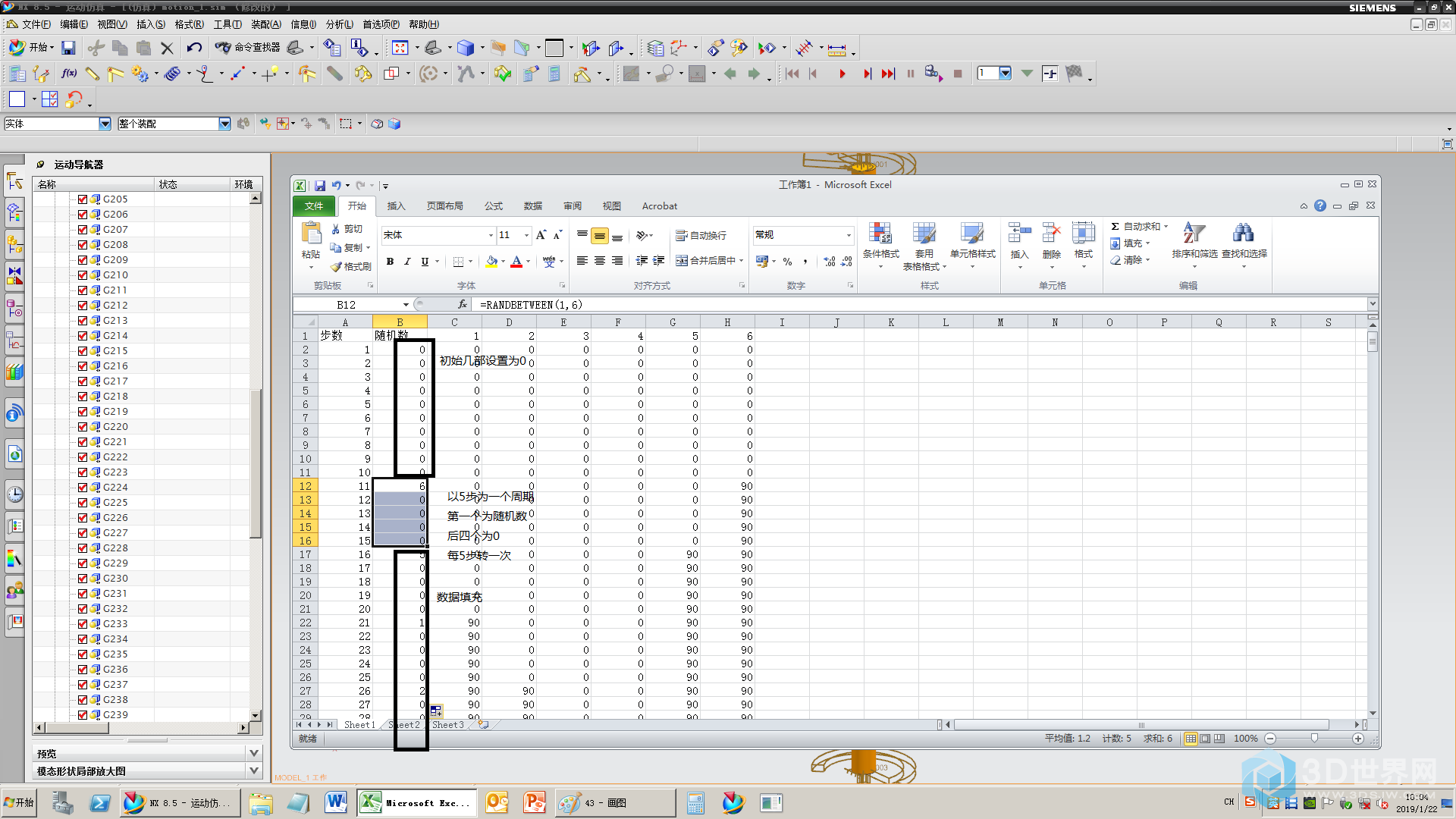
44、为了视觉效果,为了仿真稳定,前10步不动,之后每5步转一次
45、选中转轴的参数,复制一下
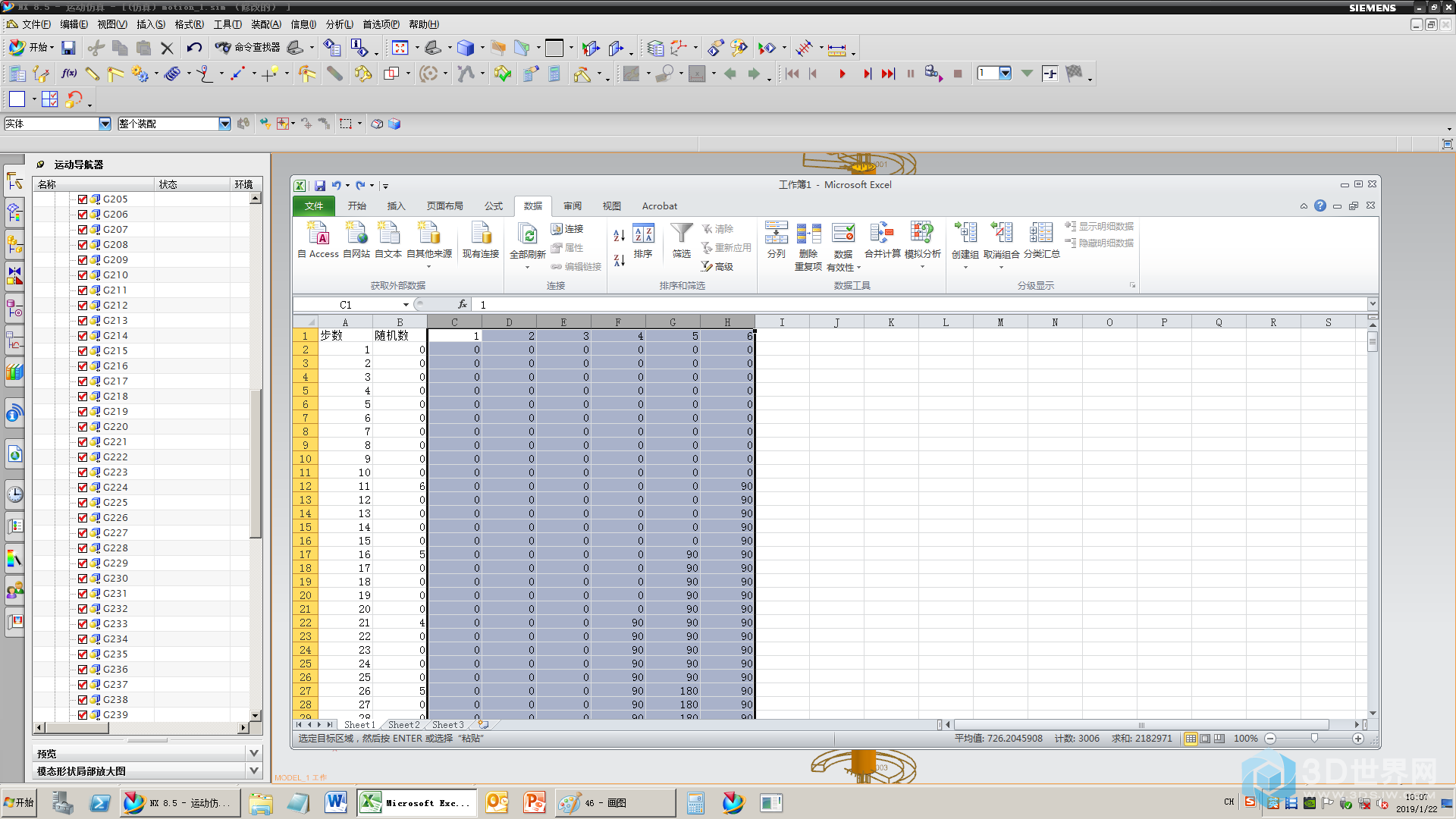
46、粘贴值
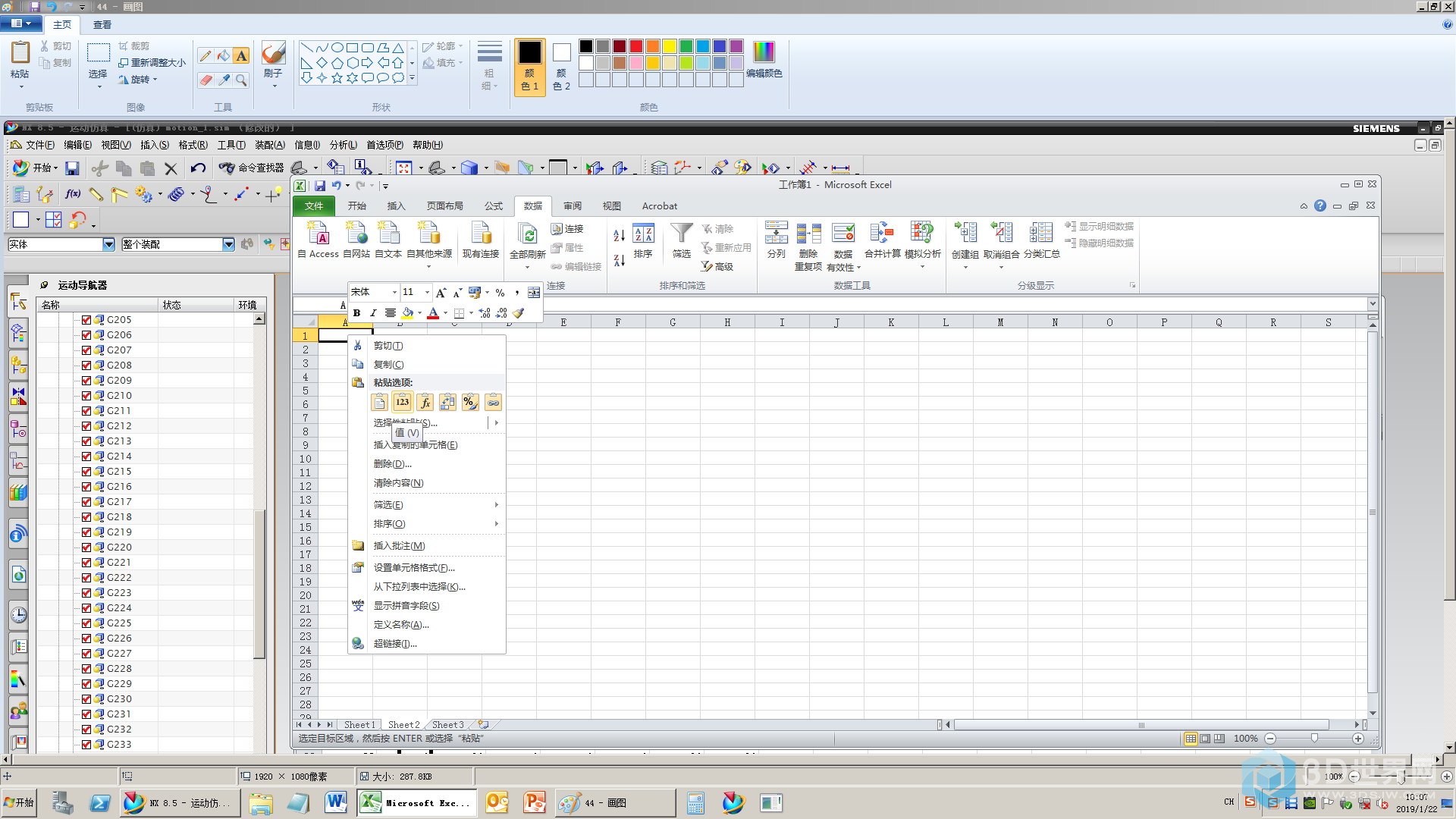
47、完成魔方转动的参数
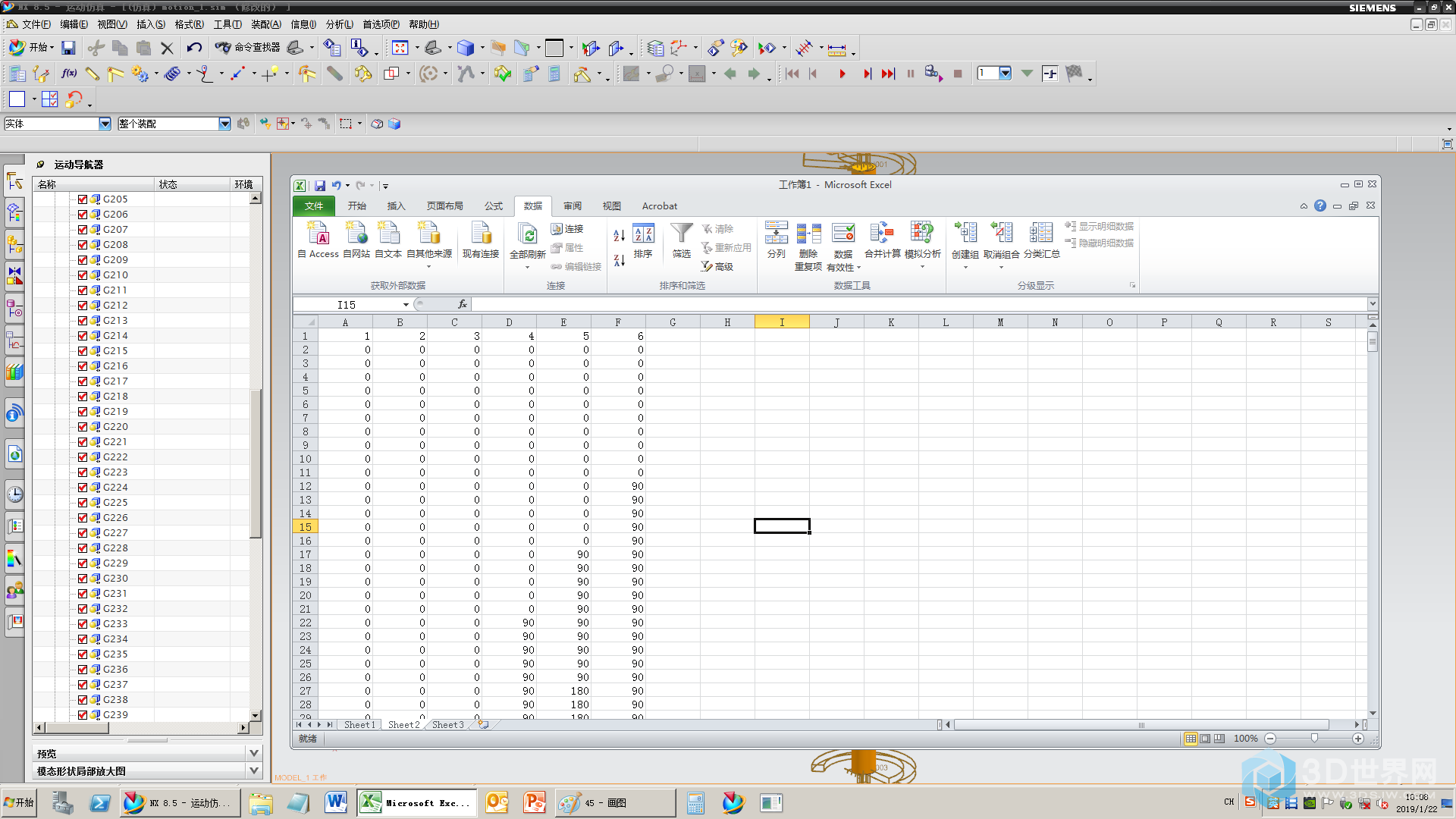
48、定义转动副的驱动,选择函数

49、选择函数管理器
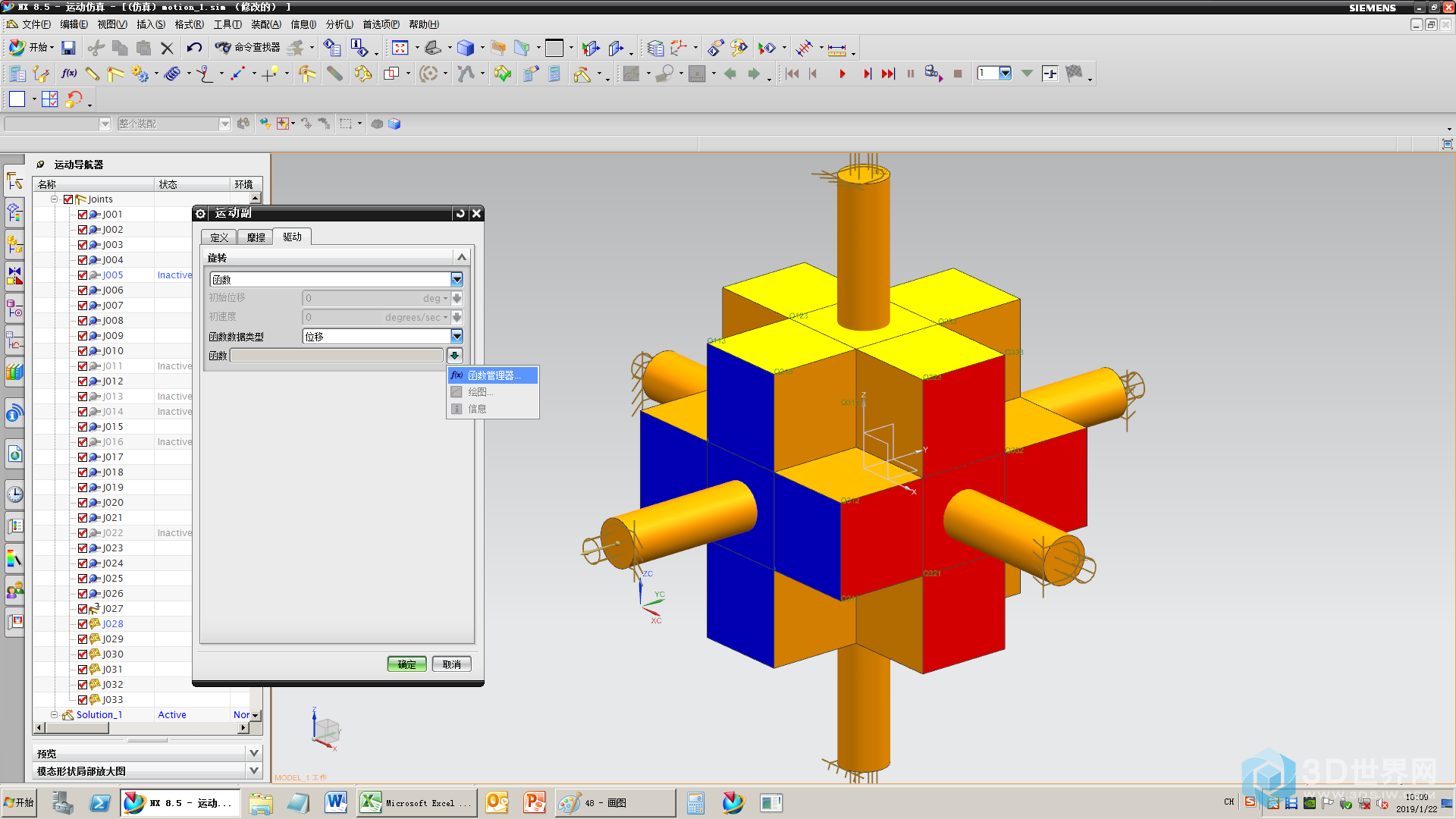
50、选择函数类型,新建函数
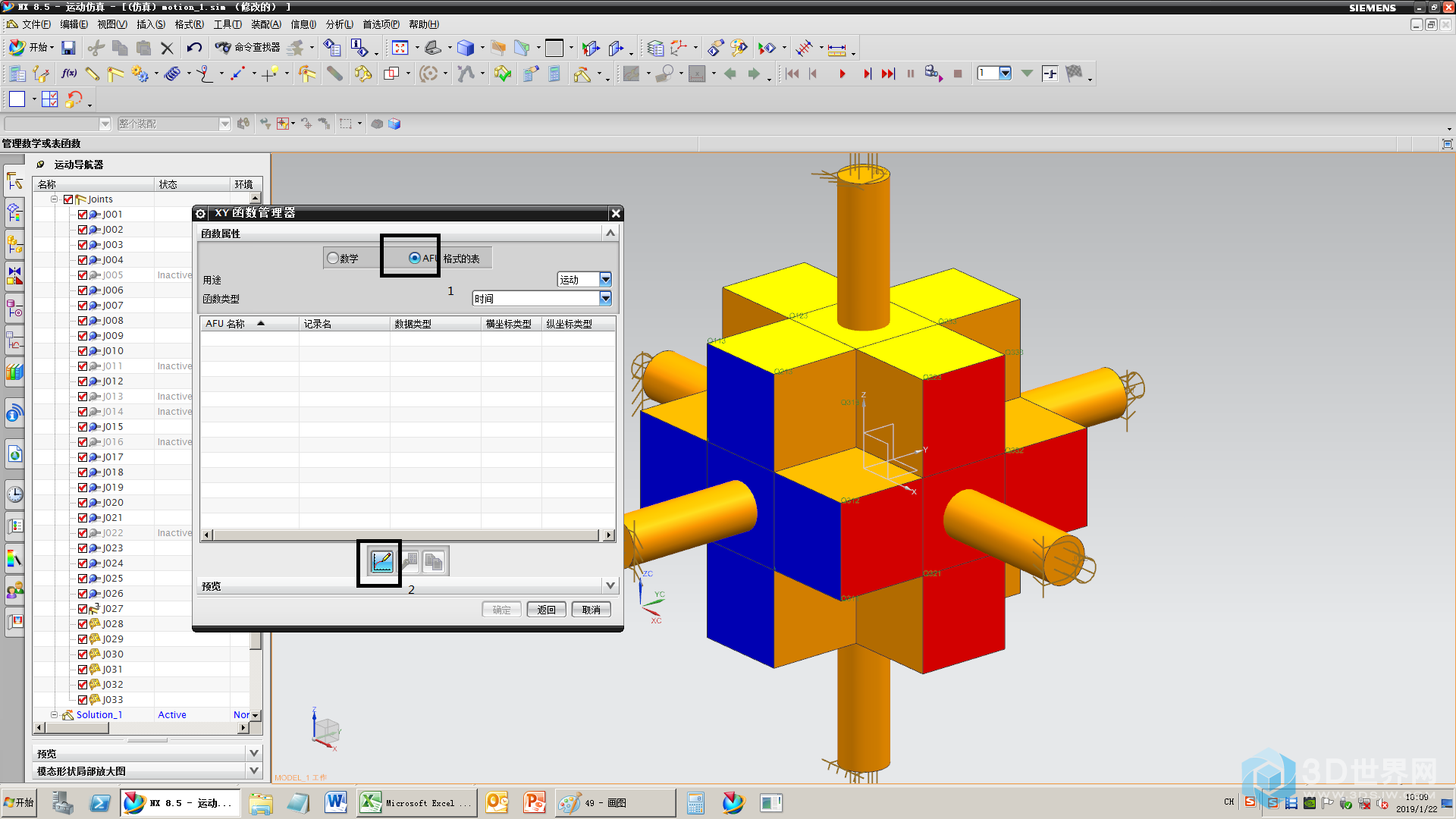
51、将excel表中的数据,复制到弹出的电子表格中
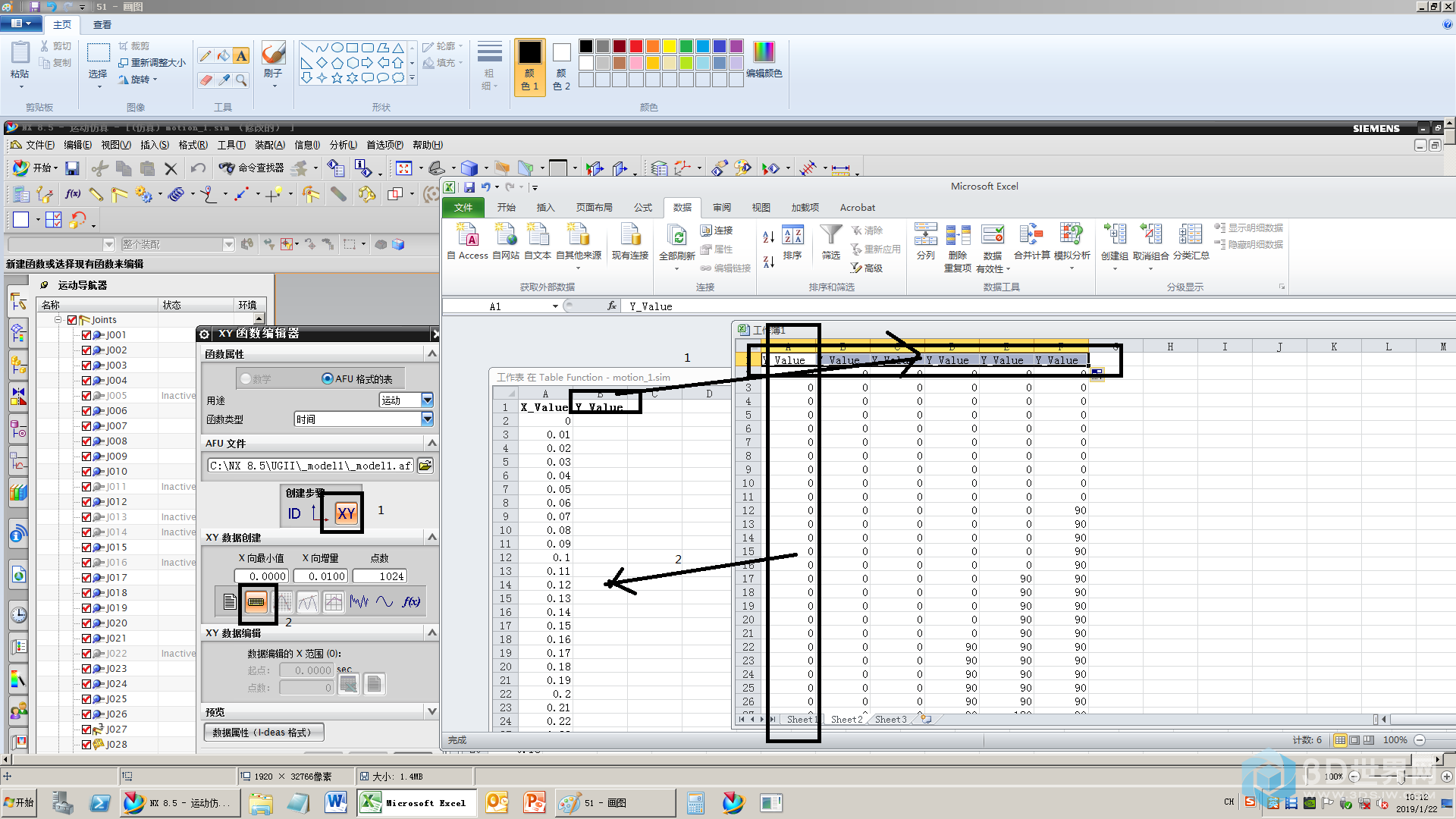
52、更新表函数
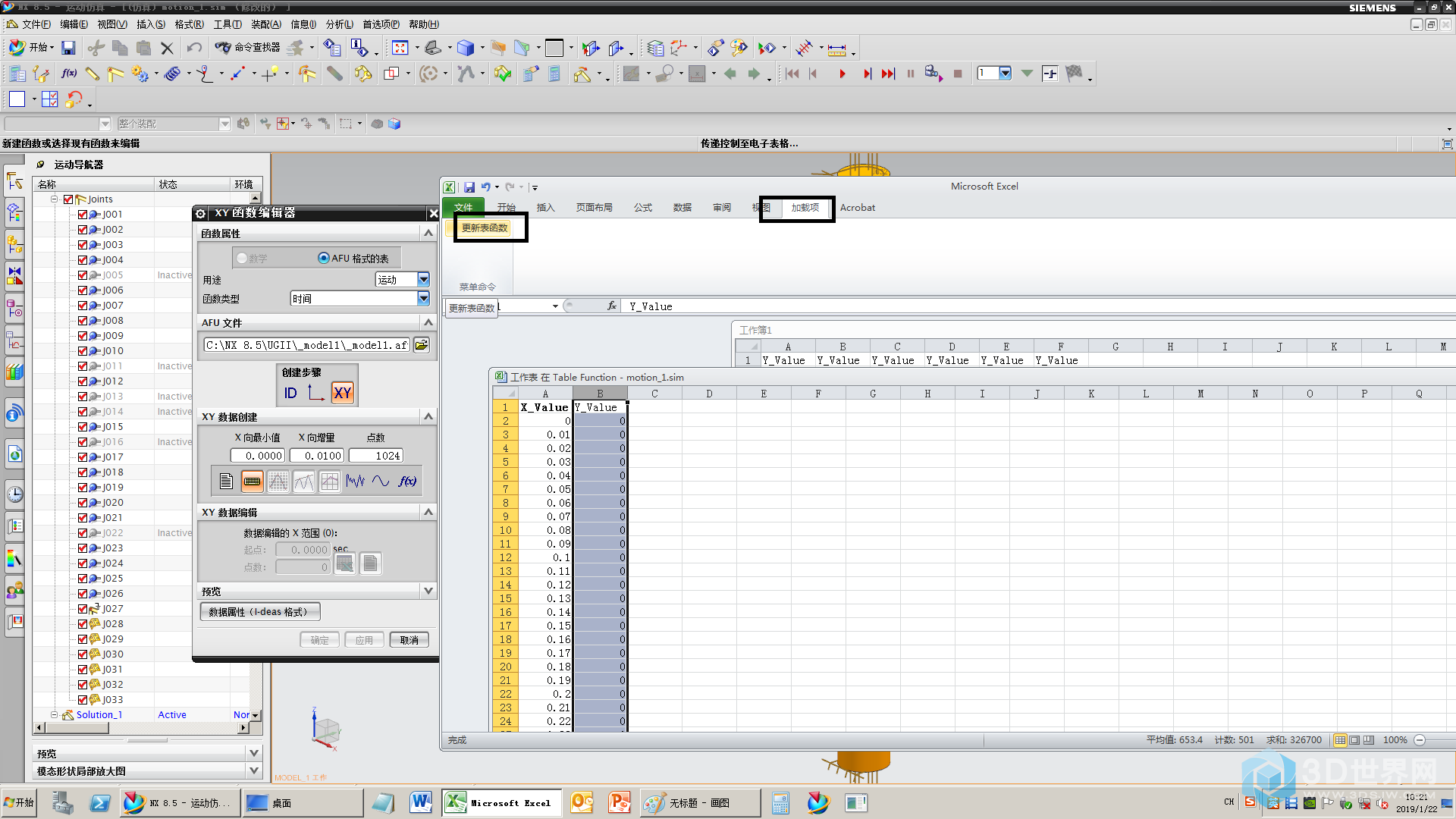
53、关闭

54、完成函数的定义
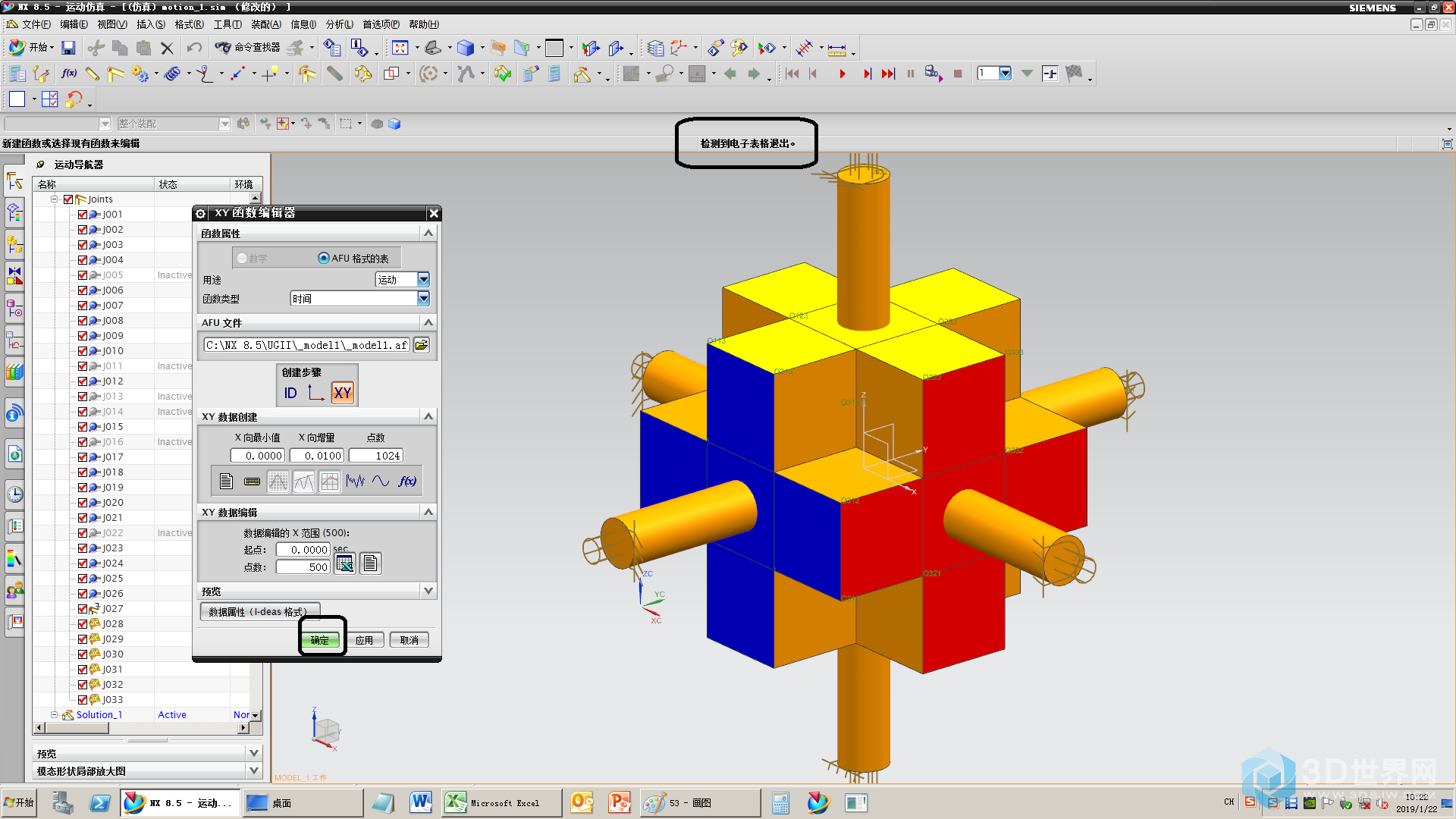
55、预览一下
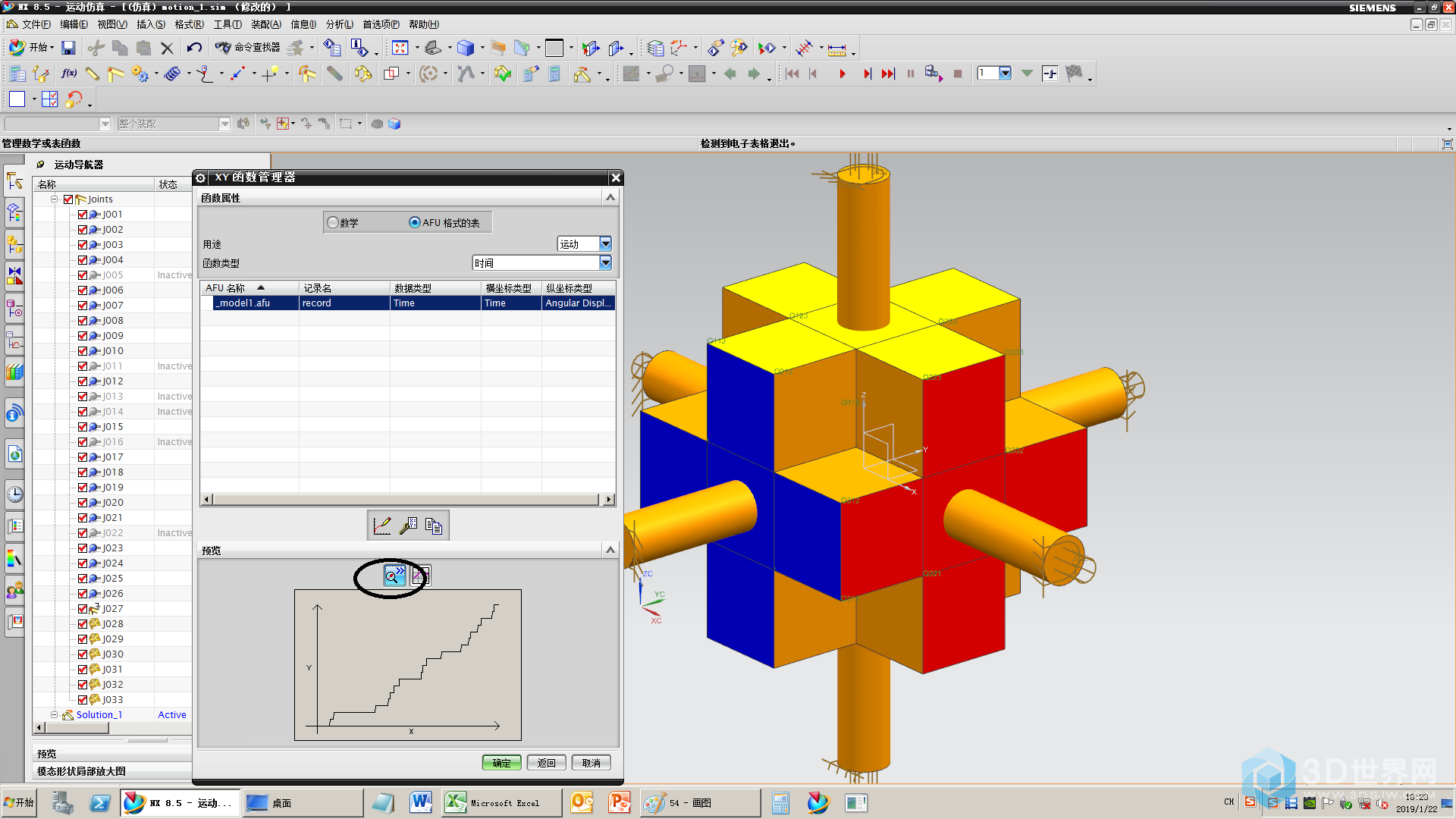
56、然后就按照相同的方式添加剩余5个轴的驱动,然后求解,(求解是可以考虑将)
补充内容 (2019-1-23 09:37):
56、然后就按照相同的方式添加剩余5个轴的驱动,然后求解,(求解是可以考虑将重力常量设置为0)
完整魔方视频见3楼 |
-

-
mofang.prt
664 KB, 下载次数: 5, 下载积分: G币 -1
-

-
mofang.part01.rar
500 KB, 下载次数: 10, 下载积分: G币 -1
-

-
mofang.part02.rar
500 KB, 下载次数: 5, 下载积分: G币 -1
-

-
mofang.part03.rar
500 KB, 下载次数: 5, 下载积分: G币 -1
-

-
mofang.part04.rar
500 KB, 下载次数: 1, 下载积分: G币 -1
-

-
mofang.part05.rar
500 KB, 下载次数: 1, 下载积分: G币 -1
-

-
mofang.part06.rar
500 KB, 下载次数: 1, 下载积分: G币 -1
-

-
mofang.part07.rar
500 KB, 下载次数: 1, 下载积分: G币 -1
-

-
mofang.part08.rar
500 KB, 下载次数: 1, 下载积分: G币 -1
-

-
mofang.part09.rar
500 KB, 下载次数: 1, 下载积分: G币 -1
-

-
mofang.part10.rar
500 KB, 下载次数: 1, 下载积分: G币 -1
-

-
mofang.part11.rar
500 KB, 下载次数: 1, 下载积分: G币 -1
-

-
mofang.part12.rar
258.05 KB, 下载次数: 2, 下载积分: G币 -1
评分
-
查看全部评分
|