|
|
最近在狂看遗传算法,这是一种经典的优化算法,我们可以把实际工程问题抽象成数学问题,变成一个含有若干未知数的函数,以及相应的约束,然后就变成了在这些约束下求这个函数的最大值或最小值的问题了,而求最大值或最小值需要用到一些优化算法,这些算法包括遗传算法,粒子群算法,蚁群算法,模拟退火算法等等等等,比如说机械中的装配线布局问题,在知道产品生产节拍,产品种类,每种产品装配工序及先后顺序,每个装配工序的运行时间的前提下,如果使得工作站的数量最少呢,工作站的数量最少也就意味着占地面积最少,投入成本最少,车间能耗最少,这个问题就可以根据产品的装配要求来把这些信息抽象成数学模型,在这个数学模型中把工作站数量设定为未知数,然后用遗传算法求这个数学模型的最小值。 这次我们用遗传算法来算一下一个函数的最大值,网上有一些类似的例子,但是经过我的查看和调试,都有些或多或少的逻辑或语法错误,经过我的不断地修改和调试,我终于调通了,下面上代码!
 f(x)=10sin(5x) 7cos(4x), 其中 x∈[0,10] .rar
(1.6 KB, 下载次数: 3)
f(x)=10sin(5x) 7cos(4x), 其中 x∈[0,10] .rar
(1.6 KB, 下载次数: 3)
这个压缩文件,是下面的函数txt文本模式,由于最后3快函数,放在论坛上面,会出现表情符号。在这里我就上传到论坛。
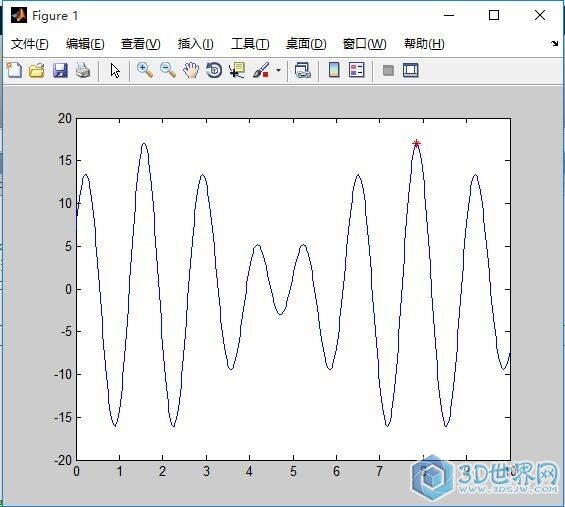
题目:求下列函数的最大值, f(x)=10*sin(5x)+7*cos(4x), 其中 x∈[0,10] 。
%Name:main.m
%主函数
clear
clf
popsize=20; %群体大小
chromlength=10; %字符串长度(个体长度)
pc=0.6; %交叉概率
pm=0.001; %变异概率
pop=initpop(popsize,chromlength); %随机产生初始群体
for i=1:20 %20为迭代次数
[objvalue]=calobjvalue(pop); %计算目标函数
fitvalue=calfitvalue(objvalue); %计算群体中每个个体的适应度
[newpop]=selection(pop,fitvalue); %复制
[newpop]=crossover(pop,pc); %交叉
[newpop]=mutation(pop,pm); %变异
[bestindividual,bestfit]=best(pop,fitvalue); %求出群体中适应值最大的个体及其适应值
y(i)=max(bestfit);
n(i)=i;
pop5=bestindividual;
x(i)=decodechrom(pop5,1,chromlength)*10/1023; %转十进制
pop=newpop;
end
fplot('10*sin(5*x)+7*cos(4*x)',[0 10])
hold on
plot(x,y,'r*')
hold off
[z index]=max(y); %计算最大值及其位置
x5=x(index)%计算最大值对应的x值
y=z
%Name: initpop.m
%初始化
function pop=initpop(popsize,chromlength)
pop=round(rand(popsize,chromlength)); % rand随机产生每个单元为 {0,1} 行数为popsize,列数为chromlength的矩阵,
% round对矩阵的每个单元进行圆整。这样产生的初始种群。
%Name: decodechrom.m
%将二进制编码转换成十进制之前对二进制位的截取,其实等你看懂这个题目时会发现对于这个例题,这个函数的功能完全可以略过
function pop2=decodechrom(pop,spoint,length)
pop1=pop(:,spoint:spoint+length-1);
pop2=decodebinary(pop1);
%Name: decodebinary.m
%将二进制转化为十进制
function pop2=decodebinary(pop)
[px,py]=size(pop); %求pop行和列数
for i=1:py
pop1(:,i)=2.^(py-i).*pop(:,i);
end
pop2=sum(pop1,2); %求pop1的每行之和
%Name: calobjvalue.m
%实现目标函数的计算
function [objvalue]=calobjvalue(pop)
temp1=decodechrom(pop,1,10); %将pop每行转化成十进制数
x=temp1*10/1023; %将二值域 中的数转化为变量域 的数
objvalue=10*sin(5*x)+7*cos(4*x); %计算目标函数值
%Name:calfitvalue.m
%计算个体的适应值
function fitvalue=calfitvalue(objvalue)
[px,py]=size(objvalue);
for i=1:px
if objvalue(i)>0
temp=objvalue(i);
else
temp=0.0;
end
fitvalue(i)=temp;
end
fitvalue=fitvalue';
%Name: selection.m
%选择复制
function [newpop]=selection(pop,fitvalue)
totalfit=sum(fitvalue); %求适应值之和
fitvalue=fitvalue/totalfit; %单个个体被选择的概率
fitvalue=cumsum(fitvalue); %如 fitvalue=[1 2 3 4],则 cumsum(fitvalue)=[1 3 6 10]
[px,py]=size(pop);
ms=sort(rand(px,1)); %从小到大排列
fitin=1;
newin=1;
while newin<=px
if(ms(newin))<fitvalue(fitin)
newpop(newin)=pop(fitin);
newin=newin+1;
else
fitin=fitin+1;
end
end



以上就是这个题目用遗传算法的解题代码了,绝对能够调试通过,只不过遗传算法是一种激励式的算法,它只有在一定概率的情况下能求得全局最优解,一般是求得局部最优解,所以这种算法的最终结果只是个参考的解,如何提高解的最优性,是无数专家学者研究的热点,对于这里例题,大家可以通过增加繁殖的代数来缓解这个问题,这个代码中只繁衍了20代,我亲自试过了,如果繁衍200代,或者2000代,甚至20000代,精度会有一定提高的。
这个代码可以适用于几乎所有一元函数的求最大值和最小值问题,这是将几个关键的地方修改一下就可以,如果是二元函数或者是多元函数的话,则需要改动的大一些,但是大部分代码都是可以直接用的,尤其是遗传过程中的,选择、交叉、变异过程,在这里代码逻辑很精彩。读者可以细细品味。
下面给大家截个最后结果图吧:
有兴趣的找我讨论啊!我们共同进步!
|
|