用粒子群算法求最大值的MATLAB程序

董垚

在公元1986年，一个叫Craig Reynolds的呆博士通过对鸟类集体觅食的这个生物行为，发明了一种经典的算法，叫粒子群算法，在我们人还没研究明白的时候，人家都开始研究鸟了，这就是人家的牛X之处啊，他发现一个鸟群外出找食物的时候，刚开始都是杂乱无章的，任意一只鸟都是以任意的速度和方向出发去找东西吃，但是找啊找啊，他们通过彼此的通讯和协作，最后总能全部集中在食物周围，基本上没有掉队的，你说这多神奇，这个呆博士通过天天的研究这些鸟找食物，发明了这种在解的空间里快速寻找全局最优解的一种方法——粒子群算法，没想到这个方法已经提出，在学术界引起了不小的轰动，引来了很多学术大咖们的围观，纷纷赞赏之余，也都纷纷在这个标准粒子群算法进行各种改进，到今天粒子群算法已经在各行各业中得到了广泛的应用，当时包括我们熟悉的机械行业。
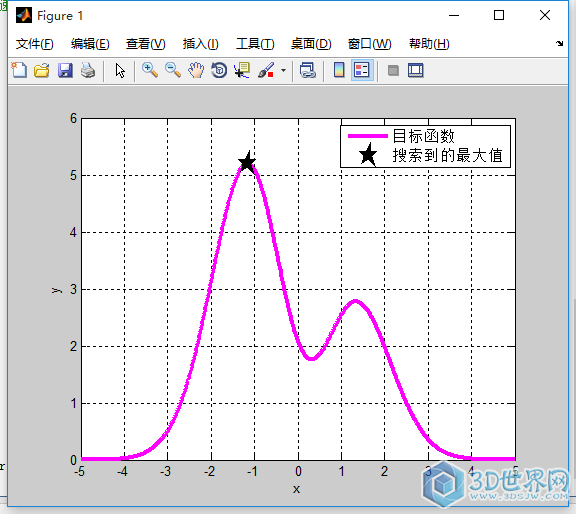
下面我们来算一个函数吧，f(x)=1+2.1(1-x+2x^2)exp(-x^2/2)，x在[-5,5]范围内，求它的最大值，怎么求，这个问题用粒子群算法来做，简直是得心应手啊，废话少说，上代码！
function main()
clc;clear all;close all;
tic;                              %程序运行计时
E0=0.001;                        %允许误差
MaxNum=100;                    %粒子最大迭代次数
narvs=1;                         %目标函数的自变量个数
particlesize=30;                    %粒子群规模
c1=2;                            %每个粒子的个体学习因子，也称为加速常数
c2=2;                            %每个粒子的社会学习因子，也称为加速常数
w=0.6;                           %惯性因子
vmax=0.8;                        %粒子的最大飞翔速度
x=-5+10*rand(particlesize,narvs);     %粒子所在的位置
v=2*rand(particlesize,narvs);         %粒子的飞翔速度
%用inline定义适应度函数以便将子函数文件与主程序文件放在一起，
%目标函数是：y=1+(2.1*(1-x+2*x.^2).*exp(-x.^2/2))
%inline命令定义适应度函数如下：
fitness=inline('1/(1+(2.1*(1-x+2*x.^2).*exp(-x.^2/2)))','x');
%inline定义的适应度函数会使程序运行速度大大降低
for i=1:particlesize
    for j=1:narvs
        f(i)=fitness(x(i,j));
    end
end

Value1=1/globalbest_faval-1; Value1=num2str(Value1);
% strcat指令可以实现字符的组合输出
disp(strcat('the maximum value','=',Value1));
%输出最大值所在的横坐标位置
Value2=globalbest_x; Value2=num2str(Value2);
disp(strcat('the corresponding coordinate','=',Value2));
x=-5:0.01:5;
y=2.1*(1-x+2*x.^2).*exp(-x.^2/2);
plot(x,y,'m-','linewidth',3);
hold on;
plot(globalbest_x,1/globalbest_faval-1,'kp','linewidth',4);
legend('目标函数','搜索到的最大值');xlabel('x');ylabel('y');grid on;toc;





这个代码我调试过，是成功的，大家谁需要用到粒子群解决工程问题的话，可以复制下来，针对自己的目标函数去修改啊。

sdgdjgb_creo

牛x。大大的牛x。

hellspint-creo

牛x。大大的牛

王绍昶

非常好，很有价值:)